Dynamics of Microvillus Extension and Tether Formation in Rolling Leukocytes

Abstract

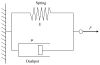
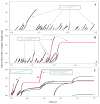
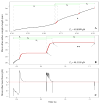
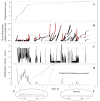
P-selectin glycoprotein ligand-1 (PSGL-1) binding to P-selectin mediates leukocyte rolling under conditions of flow. In human neutrophils, a type of leukocyte belonging to the innate immune system, PSGL-1 molecules are located on the neutrophil's surface ruffles, called microvilli. Each newly formed P-selectin-PSGL-1 bond can become load bearing, imposing on its microvillus a pulling force that deforms the microvillus. Depending on the magnitude of the bond force, a microvillus can be extended, or a thin membrane cylinder (a tether) can be formed at the tip of the microvillus. Here we propose a Kelvin-Voigt viscoelastic material as an improved model for microvillus extension. Using a modified version of our Event-Tracking Model of Adhesion (ETMA), we demonstrate how P-selectin-PSGL-1 load-bearing bonds shape microvillus deformation during neutrophil rolling at low shear (wall shear rate of 50 s(-1), P-selectin site density of 150 molecules μm(-2)). We also discuss the impact of microvillus deformability on neutrophil rolling. We find that the average microvillus extension constitutes 65% of the total microvillus-tether complex extension, and that the rolling neutrophil may never fully rest. A quantitative comparison with the corresponding non-deformable microvilli case supports a concept that the ability of the microvillus to deform stabilizes cell rolling.

Figure 1

Conceptual model non-deformable (left, A-B) and deformable (right, C-D) microvilli in the cell-substrate contact area. For simplicity only one ligand per microvillus tip is shown. L₀, ΔL, F, and F₀ are the microvillus equilibrium length, extension, bond force, and threshold bond force, respectively. ΔL_te is the tether extension. (A-B) The microvillus length is assumed to be fixed, but the microvillus can pivot about its base. At time t microvillus M₁ has a load-bearing bond, microvillus M₂ has a bond bearing no load, and microvillus M₃ has no bond. At time t + Δt the bond of M₁ is already broken, the bond of M₂ is load-bearing, and the newly formed bond of M₃ has no load yet. (C-D) Microvilli are allowed to extend and form tethers. If F < F₀ at time t, then microvillus M₁ will be longer than in A. If F > F₀ at time t + Δt, then most likely the bond of microvillus M₁ will still exist (compare D with B), the microvillus will be longer than in C, and a tether will be developed.

Figure 2

Schematic representation of a Kelvin-Voigt element. It is composed of a Hookean elastic spring of elastic modulus E and a Newtonian damper (represented here by a dashpot) of viscosity μ, connected in parallel.

Figure 3

Illustration for calculations of microvillus extension (A) and microvillus tether extension (B), for time step Δt. ΔL_old [(ΔL_te)_old] is the microvillus [tether] extension at the beginning of the time step, and ΔL_new [(ΔL_te)_new] is the microvillus [tether] extension at the end of the time step. ΔL(t) = (F/σ){1−exp[−t/(η/σ)]} and ΔL_te(t) = [(F–F₀)/η_te] t, where F, F₀, σ, and η are the microvillus bond force (assumed to be constant for the time step), threshold force, spring constant and effective viscosity, respectively. Symbol η_te denotes the effective viscosity of the microvillus tether.

Figure 4

Deformation history for all microvilli that became stressed by P-selectin—PSGL-1 load-bearing bonds during the first 1.25 seconds the sample cell rolled. The equilibrium length of each microvillus is 200 nm. (A) t < 0.35 s, (B) 0.35 s < t < 0.75 s, and (C) 0.75 < t < 1.25. The black segments represent periods of microvillus extension, and the red segments periods of tether extension. The arrows point to the curves representing the microvilli deformed by more than one load-bearing bond. The inserts indicate the number of load-bearing bonds and their overlapping pattern. The horizontal green bars symbolically illustrate the bond duration. Vertical overlapping of two bars indicates that two load-bearing bonds of a microvillus coexist for a period of time.

Figure 5

(A) Deformation history for the microvillus marked with one asterisk in Figure 4C. The lifetimes of three load-bearing bonds, B1, B2, and B3, developed by the microvillus, are represented by the green horizontal bars. F₀ is the microvillus’s threshold force. (B) Similarly, the deformation history for the microvillus marked with two asterisks in Figure 4C. The arrows point to episodes in microvillus extension which are too short to be visible in the diagram as black segments. (C) Bond force acting on the microvillus discussed in B. The dashed, horizontal line marks the microvillus threshold force.

Figure 6

Displacement (A), deformation history (B), translational velocity not filtered (C), and filtered to 60 frames per second (D), for all microvilli that became stressed by P-selectin—PSGL-1 load-bearing bonds during the first 1.25 seconds the sample cell rolled. (E) High resolution of a 0.15-second segment of data in C. (F) Data in E filtered to 60 frames per second.