Bayesian quantitative trait locus mapping using inferred haplotypes
- PMID: 20048050
- PMCID: PMC2845350
- DOI: 10.1534/genetics.109.113183
Bayesian quantitative trait locus mapping using inferred haplotypes
Abstract
We describe a fast hierarchical Bayesian method for mapping quantitative trait loci by haplotype-based association, applicable when haplotypes are not observed directly but are inferred from multiple marker genotypes. The method avoids the use of a Monte Carlo Markov chain by employing priors for which the likelihood factorizes completely. It is parameterized by a single hyperparameter, the fraction of variance explained by the quantitative trait locus, compared to the frequentist fixed-effects model, which requires a parameter for the phenotypic effect of each combination of haplotypes; nevertheless it still provides estimates of haplotype effects. We use simulation to show that the method matches the power of the frequentist regression model and, when the haplotypes are inferred, exceeds it for small QTL effect sizes. The Bayesian estimates of the haplotype effects are more accurate than the frequentist estimates, for both known and inferred haplotypes, which indicates that this advantage is independent of the effect of uncertainty in haplotype inference and will hold in comparison with frequentist methods in general. We apply the method to data from a panel of recombinant inbred lines of Arabidopsis thaliana, descended from 19 inbred founders.
Figures
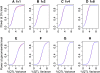


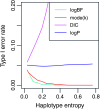


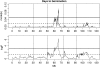
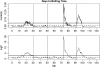
References
-
- Bardel, C., P. Darlu and E. Genin, 2006. Clustering of haplotypes based on phylogeny: How good a strategy for association testing? Eur. J. Hum. Genet. 14 202–206. - PubMed
-
- Excoffier, L., and M. Slatkin, 1995. Maximum-likelihood estimation of molecular haplotype frequencies in a diploid population. Mol. Biol. Evol. 12(5): 921–927. - PubMed
-
- Gelman, A., J. B. Carlin, H. S. Stern and D. B. Rubin, 2004. Bayesian Data Analysis, Ed. 2 (Texts in Statistical Science). Chapman & Hall/CRC, London/New York/Washington, D.C./Boca Raton, FL.
-
- Haley, C. S., and S. A. Knott, 1992. A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity 69 315–324. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

