Characteristics of transcriptional activity in nonlinear dynamics of genetic regulatory networks
- PMID: 20054406
- PMCID: PMC2796971
- DOI: 10.4137/grsb.s3119
Characteristics of transcriptional activity in nonlinear dynamics of genetic regulatory networks
Abstract
Microarray measurements of mRNA abundances is a standard tool for evaluation of transcriptional activity in functional genomics. The methodology underlying these measurements assumes existence of a direct link between transcription levels, that is, gene-specific mRNA copy numbers present in the cell, and transcription rates, that is, the numbers of gene-specific mRNA molecules synthesized per unit of time. In this paper, the question of whether or not such a tight interdependence may exist is examined in the context of nonlinear dynamics of genetic regulatory networks. Using the equations of chemical kinetics, a model has been constructed that is capable of explicitly taking into consideration nonlinear interactions between the genes through the teamwork of transcription factors. Jacobian analysis of stability has shown that steady state equilibrium is impossible in such systems. However, phase space compressibility is found to be negative, thus suggesting that asymptotic stability may exist and assume either the form of limit cycle or of a chaotic attractor. It is argued that in rapidly fluctuating or chaotic systems, direct evaluation of transcription rates through transcription levels is highly problematic. It is also noted that even if a hypothetical steady state did exist, the knowledge of transcription levels alone would not be sufficient for the evaluation of transcription rates; an additional set of parameters, namely the mRNA decay rates, would be required. An overall conclusion of the work is that the measurements of mRNA abundances are not truly representative of the functionality of genes and structural fidelity of the genetic codes.
Keywords: asymptotic stability; genetic regulatory network; jacobian eigenvalues; microarrays; nonlinear dynamics; transcription factors.
Figures
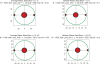
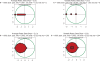
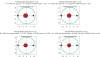
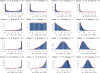
Similar articles
-
Do DNA microarrays tell the story of gene expression?Gene Regul Syst Bio. 2010 Jun 29;4:61-73. doi: 10.4137/grsb.s4657. Gene Regul Syst Bio. 2010. PMID: 20628535 Free PMC article.
-
Patterns of stochastic behavior in dynamically unstable high-dimensional biochemical networks.Gene Regul Syst Bio. 2009 Jan 29;3:1-10. doi: 10.4137/grsb.s2078. Gene Regul Syst Bio. 2009. PMID: 19838330 Free PMC article.
-
On a theory of stability for nonlinear stochastic chemical reaction networks.J Chem Phys. 2015 May 14;142(18):184101. doi: 10.1063/1.4919834. J Chem Phys. 2015. PMID: 25978877 Free PMC article.
-
Stochastic models for circadian rhythms: effect of molecular noise on periodic and chaotic behaviour.C R Biol. 2003 Feb;326(2):189-203. doi: 10.1016/s1631-0691(03)00016-7. C R Biol. 2003. PMID: 12754937 Review.
-
Stability regulation of mRNA and the control of gene expression.Ann N Y Acad Sci. 2005 Nov;1058:196-204. doi: 10.1196/annals.1359.026. Ann N Y Acad Sci. 2005. PMID: 16394137 Review.
Cited by
-
Chromosome length influences replication-induced topological stress.Nature. 2011 Mar 17;471(7338):392-6. doi: 10.1038/nature09791. Epub 2011 Mar 2. Nature. 2011. PMID: 21368764
-
Critical self-organized self-sustained oscillations in large regulatory networks: towards understanding the gene expression initiation.Gene Regul Syst Bio. 2011 Mar 22;5:27-40. doi: 10.4137/GRSB.S6804. Gene Regul Syst Bio. 2011. PMID: 21523248 Free PMC article.
-
Biomolecular self-defense and futility of high-specificity therapeutic targeting.Gene Regul Syst Bio. 2011;5:89-104. doi: 10.4137/GRSB.S8542. Epub 2011 Nov 21. Gene Regul Syst Bio. 2011. PMID: 22272063 Free PMC article.
-
Are the somatic mutation and tissue organization field theories of carcinogenesis incompatible?Cancer Inform. 2013 Dec 1;12:221-9. doi: 10.4137/CIN.S13013. eCollection 2013. Cancer Inform. 2013. PMID: 24324325 Free PMC article.
-
Systems biology and cancer: promises and perils.Prog Biophys Mol Biol. 2011 Aug;106(2):410-3. doi: 10.1016/j.pbiomolbio.2011.03.002. Epub 2011 Mar 23. Prog Biophys Mol Biol. 2011. PMID: 21419159 Free PMC article. Review.
References
-
- Schena M, Shalon D, Davis RW, Brown PO. Quantitative monitoring of gene expression patterns with a complementary DNA microarray. Science. 1995;270:467. - PubMed
-
- Shalon D, Smith SJ, Brown PO. A DNA microarray system for analyzing complex DNA samples using two-color fluorescent probe hybridization. Genome Res. 1996;6:639. - PubMed
-
- DeRisi J, et al. Use of a cDNA microarray to analyse gene expression patterns in human cancer. Nat Genet. 1996;14:457. - PubMed
-
- Lander ES. Array of hope. Nat Genet. 1999;21:3. - PubMed
LinkOut - more resources
Full Text Sources

