Modeling progression in radiation-induced lung adenocarcinomas

Abstract

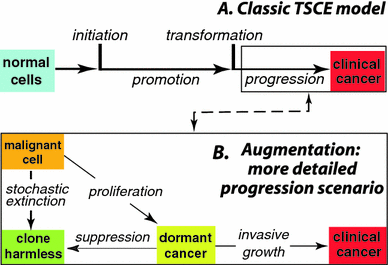
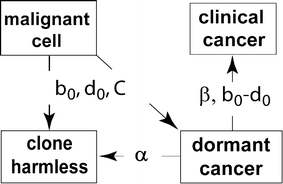
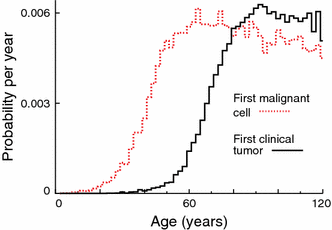
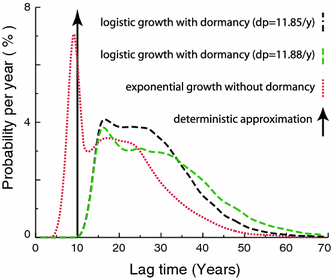
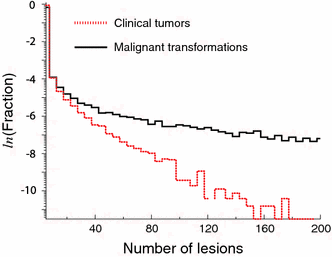
Quantitative multistage carcinogenesis models are used in radiobiology to estimate cancer risks and latency periods (time from exposure to clinical cancer). Steps such as initiation, promotion and transformation have been modeled in detail. However, progression, a later step during which malignant cells can develop into clinical symptomatic cancer, has often been approximated simply as a fixed lag time. This approach discounts important stochastic mechanisms in progression and evidence on the high prevalence of dormant tumors. Modeling progression more accurately is therefore important for risk assessment. Unlike models of earlier steps, progression models can readily utilize not only experimental and epidemiological data but also clinical data such as the results of modern screening and imaging. Here, a stochastic progression model is presented. We describe, with minimal parameterization: the initial growth or extinction of a malignant clone after formation of a malignant cell; the likely dormancy caused, for example, by nutrient and oxygen deprivation; and possible escape from dormancy resulting in a clinical cancer. It is shown, using cohort simulations with parameters appropriate for lung adenocarcinomas, that incorporating such processes can dramatically lengthen predicted latency periods. Such long latency periods together with data on timing of radiation-induced cancers suggest that radiation may influence progression itself.

Fig. 1

Carcinogenesis steps a the standard two-stage clonal expansion (TSCE) model for overall carcinogenesis. Initiation rapid alteration that produces a pre-malignant cell from the pool of normal stem cells; promotion stochastic proliferation of the pre-malignant cells; transformation a second rapid alteration which generates a malignant cell from the pool of pre-malignant cells; progression occurs during the time from the first malignant cell to clinical cancer. b More realistic model of the progression step. After transformation, a lesion may need to progress through bottlenecks, including stochastic extinction and/or dormancy, in order to generate a clinical cancer. If more than one malignant cell is formed by transformation, the different clones evolve independently of each other. For example, the second malignant cell could lead to the first clinical cancer if the first malignant clone becomes extinct, remains dormant indefinitely, or happens to grow slowly

Fig. 2

Progression parameters. The figure shows the same boxes as in Fig. 1b, specifying the clone states that are used in our model to analyze progression processes. Labels on the arrows specify the parameters relevant to transitions between these states. The parameters are fixed by experimental (not epidemiological) data and are described in more detail in the Methods section. The transition from a malignant cell to a harmless clone (shown by the downward arrow; it is actually an extinct clone in this case) is governed mainly by the maximum death rate d₀ and birth rate b ₀, with carrying capacity C playing almost no role. In the transition from dormant tumor to clinical cancer, only the difference SGR ^≡ b ₀ − d ₀ is relevant, not b₀ and d₀ seperately. In our calculations here, α was taken as 0

Fig. 3

Probability density distributions of time of first occurrence of primary malignant cells and clinical tumors in a heterogeneous cohort mimicking the atomic bomb survivor cohort. Competing risks are not taken into account. Tumor growth parameters correspond to lung adenocarcinoma. The other parameters are adjusted in order to simulate clinically observed lung cancer incidence. Fluctuations are due to using Monte-Carlo methods

Fig. 4

Stochastic progression lag time distributions (first malignant cell to first clinical tumor) for two values of the pre-malignant cell death rate d _p. For comparison, the figure also shows the lag time distribution when stochastic exponential malignant cell proliferation without dormancy is assumed and shows the delta-function distribution for a 10-year deterministic lag time model. Tumor growth parameters during progression correspond to lung adenocarcinoma; for other kinds of lung cancer (results shown in [Fakir et al. (2009) but not in the present paper] the first peak of the curve assuming no dormancy is considerably further to the left. The parameters for earlier steps (initiation, promotion, and transformation) are adjusted in order to simulate lung cancer incidence in atomic bomb survivors

Fig. 5

Predicted distribution of the number of malignant transformations and of clinical tumors that occur in the lifetime of a non-irradiated individual of age 90 years assuming the parameters computed here and no competing risks