On the spontaneous stochastic dynamics of a single gene: complexity of the molecular interplay at the promoter
- PMID: 20064204
- PMCID: PMC2832887
- DOI: 10.1186/1752-0509-4-2
On the spontaneous stochastic dynamics of a single gene: complexity of the molecular interplay at the promoter
Abstract
Background: Gene promoters can be in various epigenetic states and undergo interactions with many molecules in a highly transient, probabilistic and combinatorial way, resulting in a complex global dynamics as observed experimentally. However, models of stochastic gene expression commonly consider promoter activity as a two-state on/off system. We consider here a model of single-gene stochastic expression that can represent arbitrary prokaryotic or eukaryotic promoters, based on the combinatorial interplay between molecules and epigenetic factors, including energy-dependent remodeling and enzymatic activities.
Results: We show that, considering the mere molecular interplay at the promoter, a single-gene can demonstrate an elaborate spontaneous stochastic activity (eg. multi-periodic multi-relaxation dynamics), similar to what is known to occur at the gene-network level. Characterizing this generic model with indicators of dynamic and steady-state properties (including power spectra and distributions), we reveal the potential activity of any promoter and its influence on gene expression. In particular, we can reproduce, based on biologically relevant mechanisms, the strongly periodic patterns of promoter occupancy by transcription factors (TF) and chromatin remodeling as observed experimentally on eukaryotic promoters. Moreover, we link several of its characteristics to properties of the underlying biochemical system. The model can also be used to identify behaviors of interest (eg. stochasticity induced by high TF concentration) on minimal systems and to test their relevance in larger and more realistic systems. We finally show that TF concentrations can regulate many aspects of the stochastic activity with a considerable flexibility and complexity.
Conclusions: This tight promoter-mediated control of stochasticity may constitute a powerful asset for the cell. Remarkably, a strongly periodic activity that demonstrates a complex TF concentration-dependent control is obtained when molecular interactions have typical characteristics observed on eukaryotic promoters (high mobility, functional redundancy, many alternate states/pathways). We also show that this regime results in a direct and indirect energetic cost. Finally, this model can constitute a framework for unifying various experimental approaches. Collectively, our results show that a gene - the basic building block of complex regulatory networks - can itself demonstrate a significantly complex behavior.
Figures

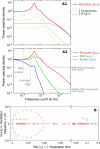
 illustrating the effect of the shot noise. (B) Each eigenvalue λi of matrix -M (or pair of conjugates) corresponds to an elementary component (or mode) in (A1) and determines its characteristics (eg. frequency and thinness of the peak). For instance, the arrows correspond to a 40 min oscillation period and a 10 s relaxation time. Colored crosses identify the components displayed in (A1). Many observables on the promoter can be described by the spectrum of -M (cf text), making it an accurate representation of the whole regulatory structure dynamics.
illustrating the effect of the shot noise. (B) Each eigenvalue λi of matrix -M (or pair of conjugates) corresponds to an elementary component (or mode) in (A1) and determines its characteristics (eg. frequency and thinness of the peak). For instance, the arrows correspond to a 40 min oscillation period and a 10 s relaxation time. Colored crosses identify the components displayed in (A1). Many observables on the promoter can be described by the spectrum of -M (cf text), making it an accurate representation of the whole regulatory structure dynamics.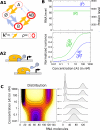
 = 20 s at both sites and 1/
= 20 s at both sites and 1/ = 60 s) and the time for DNA to loop when both sites of A are occupied is very fast 1/kclose = 1 s [93]. Concentration ranges ([10-2; 103] nM) and equilibrium constants (
= 60 s) and the time for DNA to loop when both sites of A are occupied is very fast 1/kclose = 1 s [93]. Concentration ranges ([10-2; 103] nM) and equilibrium constants ( = 20 nM and
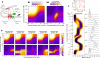
= 20 nM and  = 1 nM) were set to physiological values [79,89]. Transcription is promoted by the unlooped state, the presence of C and slightly by the presence of A at one site (see table S3 of Additional file 1 for details). RNA life-time (5 min) and abundance (between 10 and 70 copies per cell) were chosen as reported by [84,91]. (B) Exploration of the system's behavior as a function of concentrations [A] and [C] is presented in terms of mean RNA level (B1), normalized variance (B2) and distribution (C) (represented along an arbitrary path of interest because of a too large dimensionality). (D) Changing the energies of activation E0 by adding a normally distributed energy (s.d. = 3 kcal/mol) to both direction of each reaction while keeping state energies G0 unchanged does not influence the mean behavior of expression but has a profound impact on its variability. This shows that mean expression can hide most of the complexity of regulation and that stochastic aspects can reveal much kinetic information.
= 1 nM) were set to physiological values [79,89]. Transcription is promoted by the unlooped state, the presence of C and slightly by the presence of A at one site (see table S3 of Additional file 1 for details). RNA life-time (5 min) and abundance (between 10 and 70 copies per cell) were chosen as reported by [84,91]. (B) Exploration of the system's behavior as a function of concentrations [A] and [C] is presented in terms of mean RNA level (B1), normalized variance (B2) and distribution (C) (represented along an arbitrary path of interest because of a too large dimensionality). (D) Changing the energies of activation E0 by adding a normally distributed energy (s.d. = 3 kcal/mol) to both direction of each reaction while keeping state energies G0 unchanged does not influence the mean behavior of expression but has a profound impact on its variability. This shows that mean expression can hide most of the complexity of regulation and that stochastic aspects can reveal much kinetic information.
References
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Medical
Molecular Biology Databases
Miscellaneous

