Branch length estimation and divergence dating: estimates of error in Bayesian and maximum likelihood frameworks
- PMID: 20064267
- PMCID: PMC2827399
- DOI: 10.1186/1471-2148-10-5
Branch length estimation and divergence dating: estimates of error in Bayesian and maximum likelihood frameworks
Abstract
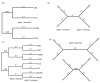
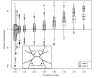
Background: Estimates of divergence dates between species improve our understanding of processes ranging from nucleotide substitution to speciation. Such estimates are frequently based on molecular genetic differences between species; therefore, they rely on accurate estimates of the number of such differences (i.e. substitutions per site, measured as branch length on phylogenies). We used simulations to determine the effects of dataset size, branch length heterogeneity, branch depth, and analytical framework on branch length estimation across a range of branch lengths. We then reanalyzed an empirical dataset for plethodontid salamanders to determine how inaccurate branch length estimation can affect estimates of divergence dates.
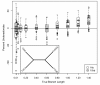
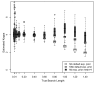
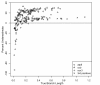
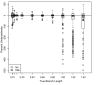
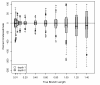
Results: The accuracy of branch length estimation varied with branch length, dataset size (both number of taxa and sites), branch length heterogeneity, branch depth, dataset complexity, and analytical framework. For simple phylogenies analyzed in a Bayesian framework, branches were increasingly underestimated as branch length increased; in a maximum likelihood framework, longer branch lengths were somewhat overestimated. Longer datasets improved estimates in both frameworks; however, when the number of taxa was increased, estimation accuracy for deeper branches was less than for tip branches. Increasing the complexity of the dataset produced more misestimated branches in a Bayesian framework; however, in an ML framework, more branches were estimated more accurately. Using ML branch length estimates to re-estimate plethodontid salamander divergence dates generally resulted in an increase in the estimated age of older nodes and a decrease in the estimated age of younger nodes.
Conclusions: Branch lengths are misestimated in both statistical frameworks for simulations of simple datasets. However, for complex datasets, length estimates are quite accurate in ML (even for short datasets), whereas few branches are estimated accurately in a Bayesian framework. Our reanalysis of empirical data demonstrates the magnitude of effects of Bayesian branch length misestimation on divergence date estimates. Because the length of branches for empirical datasets can be estimated most reliably in an ML framework when branches are <1 substitution/site and datasets are > or =1 kb, we suggest that divergence date estimates using datasets, branch lengths, and/or analytical techniques that fall outside of these parameters should be interpreted with caution.
Figures


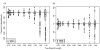


Similar articles
-
Bayesian and maximum likelihood phylogenetic analyses of protein sequence data under relative branch-length differences and model violation.BMC Evol Biol. 2005 Jan 28;5:8. doi: 10.1186/1471-2148-5-8. BMC Evol Biol. 2005. PMID: 15676079 Free PMC article.
-
The effect of ambiguous data on phylogenetic estimates obtained by maximum likelihood and Bayesian inference.Syst Biol. 2009 Feb;58(1):130-45. doi: 10.1093/sysbio/syp017. Epub 2009 May 22. Syst Biol. 2009. PMID: 20525573 Free PMC article.
-
The influence of ignoring secondary structure on divergence time estimates from ribosomal RNA genes.Mol Phylogenet Evol. 2014 Feb;71:214-23. doi: 10.1016/j.ympev.2013.12.003. Epub 2013 Dec 19. Mol Phylogenet Evol. 2014. PMID: 24361769
-
Inferences from tip-calibrated phylogenies: a review and a practical guide.Mol Ecol. 2016 May;25(9):1911-24. doi: 10.1111/mec.13586. Epub 2016 Apr 20. Mol Ecol. 2016. PMID: 26880113 Free PMC article. Review.
-
Modeling Substitution Rate Evolution across Lineages and Relaxing the Molecular Clock.Genome Biol Evol. 2024 Sep 3;16(9):evae199. doi: 10.1093/gbe/evae199. Genome Biol Evol. 2024. PMID: 39332907 Free PMC article. Review.
Cited by
-
Winding up the molecular clock in the genus Carabus (Coleoptera: Carabidae): assessment of methodological decisions on rate and node age estimation.BMC Evol Biol. 2012 Mar 28;12:40. doi: 10.1186/1471-2148-12-40. BMC Evol Biol. 2012. PMID: 22455387 Free PMC article.
-
Advantages of an easy-to-use DNA extraction method for minimal-destructive analysis of collection specimens.PLoS One. 2020 Jul 8;15(7):e0235222. doi: 10.1371/journal.pone.0235222. eCollection 2020. PLoS One. 2020. PMID: 32639972 Free PMC article.
-
Circadian input kinases and their homologs in cyanobacteria: evolutionary constraints versus architectural diversification.J Mol Evol. 2010 May;70(5):453-65. doi: 10.1007/s00239-010-9344-0. Epub 2010 May 1. J Mol Evol. 2010. PMID: 20437037
-
Variation in DNA substitution rates among lineages erroneously inferred from simulated clock-like data.PLoS One. 2010 Mar 11;5(3):e9649. doi: 10.1371/journal.pone.0009649. PLoS One. 2010. PMID: 20300176 Free PMC article.
-
Potential for bias and low precision in molecular divergence time estimation of the Canopy of Life: an example from aquatic bird families.Front Genet. 2015 Jun 8;6:203. doi: 10.3389/fgene.2015.00203. eCollection 2015. Front Genet. 2015. PMID: 26106406 Free PMC article.
References
-
- Pennington RT, Lavin M, Prado DE, Pendry CA, Pell SK, Butterworth CA. Historical climate change and speciation: neotropical seasonally dry forest plants show patterns of both tertiary and quaternary diversification. Philos Trans R Soc Lond B Biol Sci. 2004;359(1443):515–537. doi: 10.1098/rstb.2003.1435. - DOI - PMC - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

