Reaction factoring and bipartite update graphs accelerate the Gillespie Algorithm for large-scale biochemical systems
- PMID: 20066048
- PMCID: PMC2798956
- DOI: 10.1371/journal.pone.0008125
Reaction factoring and bipartite update graphs accelerate the Gillespie Algorithm for large-scale biochemical systems
Abstract
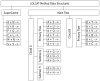
ODE simulations of chemical systems perform poorly when some of the species have extremely low concentrations. Stochastic simulation methods, which can handle this case, have been impractical for large systems due to computational complexity. We observe, however, that when modeling complex biological systems: (1) a small number of reactions tend to occur a disproportionately large percentage of the time, and (2) a small number of species tend to participate in a disproportionately large percentage of reactions. We exploit these properties in LOLCAT Method, a new implementation of the Gillespie Algorithm. First, factoring reaction propensities allows many propensities dependent on a single species to be updated in a single operation. Second, representing dependencies between reactions with a bipartite graph of reactions and species requires only storage for reactions, rather than the required for a graph that includes only reactions. Together, these improvements allow our implementation of LOLCAT Method to execute orders of magnitude faster than currently existing Gillespie Algorithm variants when simulating several yeast MAPK cascade models.
Conflict of interest statement
Figures
Similar articles
-
Hybrid deterministic/stochastic simulation of complex biochemical systems.Mol Biosyst. 2017 Nov 21;13(12):2672-2686. doi: 10.1039/c7mb00426e. Mol Biosyst. 2017. PMID: 29058744
-
Slow update stochastic simulation algorithms for modeling complex biochemical networks.Biosystems. 2017 Dec;162:135-146. doi: 10.1016/j.biosystems.2017.10.011. Epub 2017 Nov 1. Biosystems. 2017. PMID: 29080799
-
Accelerating rejection-based simulation of biochemical reactions with bounded acceptance probability.J Chem Phys. 2016 Jun 14;144(22):224108. doi: 10.1063/1.4953559. J Chem Phys. 2016. PMID: 27305997
-
Efficient Constant-Time Complexity Algorithm for Stochastic Simulation of Large Reaction Networks.IEEE/ACM Trans Comput Biol Bioinform. 2017 May-Jun;14(3):657-667. doi: 10.1109/TCBB.2016.2530066. Epub 2016 Feb 15. IEEE/ACM Trans Comput Biol Bioinform. 2017. PMID: 26890923
-
Temporal Gillespie Algorithm: Fast Simulation of Contagion Processes on Time-Varying Networks.PLoS Comput Biol. 2015 Oct 30;11(10):e1004579. doi: 10.1371/journal.pcbi.1004579. eCollection 2015 Oct. PLoS Comput Biol. 2015. PMID: 26517860 Free PMC article.
Cited by
-
Multi-scale stochastic simulation of diffusion-coupled agents and its application to cell culture simulation.PLoS One. 2011;6(12):e29298. doi: 10.1371/journal.pone.0029298. Epub 2011 Dec 21. PLoS One. 2011. PMID: 22216238 Free PMC article.
-
Multi-scale models of whole cells: progress and challenges.Front Cell Dev Biol. 2023 Nov 7;11:1260507. doi: 10.3389/fcell.2023.1260507. eCollection 2023. Front Cell Dev Biol. 2023. PMID: 38020904 Free PMC article. Review.
-
Simulation and inference algorithms for stochastic biochemical reaction networks: from basic concepts to state-of-the-art.J R Soc Interface. 2019 Feb 28;16(151):20180943. doi: 10.1098/rsif.2018.0943. J R Soc Interface. 2019. PMID: 30958205 Free PMC article.
References
-
- Gillespie D. Exact stochastic simulation of coupled chemical reactions. Journal of Physical Chemistry. 1977;81:2309–2586.
-
- Cao Y, Li H, Petzold L. Efficient formulation of the stochastic simulation algorithm for chemically reacting systems. Journal of Physical Chemistry. 2004;121:4059–4067. - PubMed
-
- Gibson M, Bruck J. Efficient exact stochastic simulation of chemical systems with many species and many channels. Journal of Physical Chemistry A. 2000;104:1876–1889.
-
- Indurkhya S, Beal J. Code for lolcat method. 2009. MIT Dspace: http://hdl.handle.net/1721.1/46710.
-
- Gillespie D, Petzold L. Improved leap-size selection for accelerated stochastic simulation. Journal of Chemical Physics. 2003;119:8229–8234.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

