Stochastic bistability and bifurcation in a mesoscopic signaling system with autocatalytic kinase
- PMID: 20074511
- PMCID: PMC2800974
- DOI: 10.1016/j.bpj.2009.09.055
Stochastic bistability and bifurcation in a mesoscopic signaling system with autocatalytic kinase
Abstract
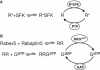
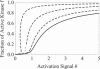
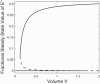
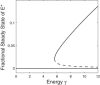
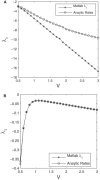
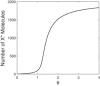
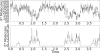
Bistability is a nonlinear phenomenon widely observed in nature including in biochemical reaction networks. Deterministic chemical kinetics studied in the past has shown that bistability occurs in systems with strong (cubic) nonlinearity. For certain mesoscopic, weakly nonlinear (quadratic) biochemical reaction systems in a small volume, however, stochasticity can induce bistability and bifurcation that have no macroscopic counterpart. We report the simplest yet known reactions involving driven phosphorylation-dephosphorylation cycle kinetics with autocatalytic kinase. We show that the noise-induced phenomenon is correlated with free energy dissipation and thus conforms with the open-chemical system theory. A previous reported noise-induced bistability in futile cycles is found to have originated from the kinase synchronization in a bistable system with slow transitions, as reported here.
Copyright 2010 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures


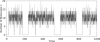


References
-
- Pearson H. Cell biology: the cellular hullabaloo. Nature. 2008;453:150–153. - PubMed
-
- Süel G.M., Kulkarni R.P., Elowitz M.B. Tunability and noise dependence in differentiation dynamics. Science. 2007;315:1716–1719. - PubMed
-
- Kaern M., Elston T.C., Collins J.J. Stochasticity in gene expression: from theories to phenotypes. Nat. Rev. Genet. 2005;6:451–464. - PubMed
-
- Paulsson J. Models of stochastic gene expression. Phys. Life Rev. 2005;2:157–175.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Miscellaneous

