A comparison of regression techniques for a two-dimensional sensorimotor rhythm-based brain-computer interface

Abstract

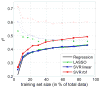
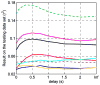
People can learn to control electroencephalogram (EEG) features consisting of sensorimotor-rhythm amplitudes and use this control to move a cursor in one, two or three dimensions to a target on a video screen. This study evaluated several possible alternative models for translating these EEG features into two-dimensional cursor movement by building an offline simulation using data collected during online performance. In offline comparisons, support-vector regression (SVM) with a radial basis kernel produced somewhat better performance than simple multiple regression, the LASSO or a linear SVM. These results indicate that proper choice of a translation algorithm is an important factor in optimizing brain-computer interface (BCI) performance, and provide new insight into algorithm choice for multidimensional movement control.

Figure 1

Left: EEG recorded from two electrodes during one trial. At zero time the target appears. One sec later the cursor appears and begins to move. One of the sliding windows is highlighted in red. Center: Hypothetical example showing the eight possible target locations, and the target for the current trial (in green). The green (gray) curve represents the cursor movement generated by the offline analysis up to (after) the time of the red window. The red sliding window must be used to move the red dot. Right: The sigmoid function. If the target if far from the cursor, the exact relative position of the target does not mater, just the direction is important. This is why, for example, the output for the relative coordinate of (0.5; 0.5) is very close to the one of (1; 1), meaning that in both cases the user should move fast to the right and to the top.

Figure 2

Holdout: one data set is used for training (gray) and the other for testing (red). Cross Validation: the data are split into n parts. A total of n analyses are performed. Each part is used as the testing set (red) for one analysis while the n−1 other parts are used as the training set (gray). To adjust the parameters, a second level of cross validation is made: before each of the n analysis, n−1 analyses are made (training sets are in grey and testing sets in blue). To obtain unbiased result, the testing data set of the first level of cross validation (red) is not used during the second level of cross validation (white).

Figure 3

Results on the training (dash lines) and testing (full lines) data sets in term of the square of Pearson’s correlation coefficient as a function of the size of the training data set for the four different methods.

Figure 4

Results on the testing data set (as r²) as a function of the delay. Each user is represented by a different color. The two users with spinal cord injuries are represented by dash lines. The right end of the curves is with an infinite delay (i.e., the previous cursor movement is not taken into account, so that the desired output of the regression is the absolute coordinate of the target and does not depend on the cursor position). (The multiple linear regression technique was used with the sliding windows approach, two electrodes and features selection.)

Figure 5

Average results in term of r² for eight users (with the multiple linear regression technique, the sliding windows approach, two electrodes and features selection), when no interpolation is used (dark blue) and for four different interpolation methods. The error bars represent the interval of confidence at 95% of the increase of the results compare to no interpolation. Except for the nearest neighbor, all the interpolation techniques significantly increase the results.

Figure 6

Average results (as r²) for eight users, for multiple linear regression (M.L.R.) and SVR with RBF kernel, when working on sliding windows. Feature-unique weights for the RBF were calculated by the feature selection algorithm. The error bars represent the interval of confidence at 95% of the increase of the results compare to MLR with 10 electrodes and no features selection. The starts show methods significantly different from 10 electrodes and no feature selection.