The mechanical properties of single fibrin fibers

Abstract

Summary background: Blood clots perform the mechanical task of stemming the flow of blood.

Objectives: To advance understanding and realistic modeling of blood clot behavior we determined the mechanical properties of the major structural component of blood clots, fibrin fibers.

Methods: We used a combined atomic force microscopy (AFM)/fluorescence microscopy technique to determine key mechanical properties of single crosslinked and uncrosslinked fibrin fibers.

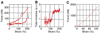
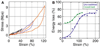
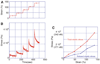
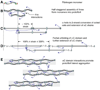
Results and conclusions: Overall, full crosslinking renders fibers less extensible, stiffer, and less elastic than their uncrosslinked counterparts. All fibers showed stress relaxation behavior (time-dependent weakening) with a fast and a slow relaxation time, 2 and 52 s. In detail, crosslinked and uncrosslinked fibrin fibers can be stretched to 2.5 and 3.3 times their original length before rupturing. Crosslinking increased the stiffness of fibers by a factor of 2, as the total elastic modulus, E(0), increased from 3.9 to 8.0 MPa and the relaxed, elastic modulus, E(infinity), increased from 1.9 to 4.0 MPa upon crosslinking. Moreover, fibers stiffened with increasing strain (strain hardening), as E(0) increased by a factor of 1.9 (crosslinked) and 3.0 (uncrosslinked) at strains epsilon > 110%. At low strains, the portion of dissipated energy per stretch cycle was small (< 10%) for uncrosslinked fibers, but significant (approximately 40%) for crosslinked fibers. At strains > 100%, all fiber types dissipated about 70% of the input energy. We propose a molecular model to explain our data. Our single fiber data can now also be used to construct a realistic, mechanical model of a fibrin network.

Fig. 1. Experimental set-up

(A) Schematic of atomic force microscope (AFM) sitting on top of the inverted optical microscope. (B) Top view of stretched fiber. The initial and stretched states are in dotted gray and solid black, respectively. (C) Typical fibrin fiber stress–strain curve. (D–F) Fluorescence microscopy movie frames of a stretching experiment. The fiber is anchored on two ridges (brighter, horizontal, 8 µm wide bars) and suspended over a groove (darker, horizontal, 12 µm wide bars); the AFM cantilever appears as a 35 µm wide, dark rectangle; the AFM tip is indicated as a green dot.

Fig. 2. Strain hardening

(A) Stress–strain curve of an uncrosslinked fibrin fiber. (B) The total elastic modulus, E₀ [slope of forward curve in (A)] as a function of strain. (C) Stress–strain curve for a crosslinked fibrin fiber.

Fig. 3. Energy loss

(A) Stress–strain curve for three consecutive pulls of uncrosslinked fiber with strains of 48%, 85% and 125%. The energy loss corresponds to the area inscribed in a cyclical stress–strain curve. (B) Ratio (percentage) of energy lost vs. total energy for crosslinked fibers (gray) and uncrosslinked fibers (black). Sigmoidal fitting curves of the form $R=R_1+\frac{R_2-R_1}{1+{\mathrm{e}}^{-\frac{\mathrm{\epsilon }-{\mathrm{\epsilon }}_0}{s}}},$ were used to fit the data. R₁ is the initial value, R₂ is the final value, ε₀ is the strain at the inflection point.

Fig. 4. Incremental stress–strain curves

(A) Strain vs. time and (B) stress vs. time for an incremental stress–strain curve of a fibrin fiber. The x-axis (time) is the same for (A) and (B). The strain is held constant at 23%, 46%, 75%, 104%and 138% for about 120 s. The stress decays exponentially at each strain value. (C) Total stress (squares) and relaxed stress (dots) vs. strain as obtained from the data in (A) and (B).

Fig. 5. Model for fibrin fiber extensions

(A) Crystal structure of fibrinogen [8]; the Aa chains, Bb chains and c chains are in blue, red and green, respectively (please see the online version of this article for figure colors). A cartoon depiction of the flexible aC region is added to the crystal structure as a blue line and blue square; aC regions may interact with each other within a protofibril, and across protofibrils. (B) Schematic model of halfstaggered assembly of three fibrin monomers into protofibril (b-nodule is no longer depicted). (C) An a-helix to b-strand conversion of the coiled coil and a slight straightening and alignment of the molecules could accommodate approximately 100% strain. Some of the aC regions are also extended at this point. (D) Higher strains, up to 320% could be accommodated by a partial unfolding of the globular c-nodule; 230% strain is depicted. Further extension of the aC region could occur. (E) Interactions between aC regions promote lateral aggregation of protofibrils; they can be elastically extended.