Mechanical buckling of veins under internal pressure

Abstract

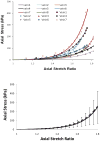
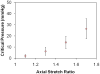
Venous tortuosity is associated with multiple disease states and is often thought to be a consequence of venous hypertension and chronic venous disease. However, the underlying mechanisms of vein tortuosity are unclear. We hypothesized that increased pressure causes vein buckling that leads to a tortuous appearance. The specific aim of this study was to determine the critical buckling pressure of veins. We determined the buckling pressure of porcine jugular veins and measured the mechanical properties of these veins. Our results showed that the veins buckle when the transmural pressure exceeds a critical pressure that is strongly related to the axial stretch ratio in the veins. The critical pressures of the eight veins tested were 14.2 +/- 5.4 and 26.4 +/- 9.0 mmHg at axial stretch ratio 1.5 and 1.7, respectively. In conclusion, veins buckle into a tortuous shape at high lumen pressures or reduced axial stretch ratios. Our results are useful in understanding the development of venous tortuosity associated with varicose veins, venous valvular insufficiency, diabetic retinopathy, and vein grafts.

Figure 1

Schematic illustrating the experimental set ups for vein inflation tests. Vein segments mounted in the tissue chamber were inflated with PBS using a syringe pump while the deformation was captured by the camera.

Figure 2

Deformation of an internal jugular vein expands freely under internal pressure. Top: pressure = 4 mmHg, Middle: pressure =50 mmHg. Bottom: the axial and circumferential stretch ratios plotted as functions of lumen pressure.

Figure 2

Deformation of an internal jugular vein expands freely under internal pressure. Top: pressure = 4 mmHg, Middle: pressure =50 mmHg. Bottom: the axial and circumferential stretch ratios plotted as functions of lumen pressure.

Figure 3

Axial stress plotted with the axial stretch ratio for eight veins underwent pressurized inflation test. The top panel illustrated comparisons of the experimental data (symbols) and the fitting curves in form of equation (4). The bottom panel illustrated the mean value of the eight veins with the error bars represent the standard deviation. The dotted line is the curve generated using the mean values of material constants α and β (see Table 2).

Figure 4

A jugular vein under internal pressure. Top: internal pressure =2 mmHg; Middle: internal pressure = 8 mmHg; and bottom: internal pressure =20 mmHg. The axial stretched ratio was 1.5 and the critical pressure was 14 mmHg. Note that this is the same vein as shown in Figure 2.

Figure 5

Deflection to length ratio of eight veins plotted as functions of internal pressure normalized by the critical pressure.

Figure 6

Critical buckling pressure of eight veins (mean ± SD) plotted as a function of the axial stretch ratio. The critical pressure increases with increasing axial stretch ratio.

Figure 7

Comparisons of critical buckling pressures of six veins measured experimentally (solid diamonds) and predicted from the buckling equations (hollow symbols). The hollow triangles represent model predictions using the average modulus. The hollow circles represent model predictions using the exponential stress strain curve and the corresponding incremental modulus. See text for details.