Fast, accurate photon beam accelerator modeling using BEAMnrc: a systematic investigation of efficiency enhancing methods and cross-section data

Abstract

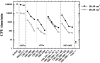
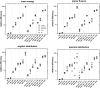
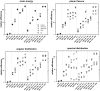
In this work, an investigation of efficiency enhancing methods and cross-section data in the BEAMnrc Monte Carlo (MC) code system is presented. Additionally, BEAMnrc was compared with VMC++, another special-purpose MC code system that has recently been enhanced for the simulation of the entire treatment head. BEAMnrc and VMC++ were used to simulate a 6 MV photon beam from a Siemens Primus linear accelerator (linac) and phase space (PHSP) files were generated at 100 cm source-to-surface distance for the 10 x 10 and 40 x 40 cm2 field sizes. The BEAMnrc parameters/techniques under investigation were grouped by (i) photon and bremsstrahlung cross sections, (ii) approximate efficiency improving techniques (AEITs), (iii) variance reduction techniques (VRTs), and (iv) a VRT (bremsstrahlung photon splitting) in combination with an AEIT (charged particle range rejection). The BEAMnrc PHSP file obtained without the efficiency enhancing techniques under study or, when not possible, with their default values (e.g., EXACT algorithm for the boundary crossing algorithm) and with the default cross-section data (PEGS4 and Bethe-Heitler) was used as the "base line" for accuracy verification of the PHSP files generated from the different groups described previously. Subsequently, a selection of the PHSP files was used as input for DOSXYZnrc-based water phantom dose calculations, which were verified against measurements. The performance of the different VRTs and AEITs available in BEAMnrc and of VMC++ was specified by the relative efficiency, i.e., by the efficiency of the MC simulation relative to that of the BEAMnrc base-line calculation. The highest relative efficiencies were approximately 935 (approximately 111 min on a single 2.6 GHz processor) and approximately 200 (approximately 45 min on a single processor) for the 10 x 10 field size with 50 million histories and 40 x 40 cm2 field size with 100 million histories, respectively, using the VRT directional bremsstrahlung splitting (DBS) with no electron splitting. When DBS was used with electron splitting and combined with augmented charged particle range rejection, a technique recently introduced in BEAMnrc, relative efficiencies were approximately 420 (approximately 253 min on a single processor) and approximately 175 (approximately 58 min on a single processor) for the 10 x 10 and 40 x 40 cm2 field sizes, respectively. Calculations of the Siemens Primus treatment head with VMC++ produced relative efficiencies of approximately 1400 (approximately 6 min on a single processor) and approximately 60 (approximately 4 min on a single processor) for the 10 x 10 and 40 x 40 cm2 field sizes, respectively. BEAMnrc PHSP calculations with DBS alone or DBS in combination with charged particle range rejection were more efficient than the other efficiency enhancing techniques used. Using VMC++, accurate simulations of the entire linac treatment head were performed within minutes on a single processor. Noteworthy differences (+/- 1%-3%) in the mean energy, planar fluence, and angular and spectral distributions were observed with the NIST bremsstrahlung cross sections compared with those of Bethe-Heitler (BEAMnrc default bremsstrahlung cross section). However, MC calculated dose distributions in water phantoms (using combinations of VRTs/AEITs and cross-section data) agreed within 2% of measurements. Furthermore, MC calculated dose distributions in a simulated water/air/water phantom, using NIST cross sections, were within 2% agreement with the BEAMnrc Bethe-Heitler default case.

Figure 1

CPU time (log scale) spent generating phase space files at 100 cm SSD for the 10×10 and 40×40 cm² field sizes, using VMC++ and the different AEITs and VRTs available in BEAMnrc (see Table 1). CPU time is scaled to that of a single 2.6 GHz Opteron processor. The label “default” refers to BEAMnrc simulation using default parameters∕techniques.

Figure 2

(a) Mean energy, (b) planar fluence, and (c) angular and (d) spectral distributions for BEAMnrc with BH (default) and with NIST bremsstrahlung cross sections and for the 10×10 and 40×40 cm² field sizes. The percentage difference between BEAMnrc with the default parameters∕techniques and NIST, DBS combined with photon forcing (DBS 1000+PF 5), DBS combined with augmented charged particle range rejection (DBS 1000+ARR), and VMC++ is also shown.

Figure 2

(a) Mean energy, (b) planar fluence, and (c) angular and (d) spectral distributions for BEAMnrc with BH (default) and with NIST bremsstrahlung cross sections and for the 10×10 and 40×40 cm² field sizes. The percentage difference between BEAMnrc with the default parameters∕techniques and NIST, DBS combined with photon forcing (DBS 1000+PF 5), DBS combined with augmented charged particle range rejection (DBS 1000+ARR), and VMC++ is also shown.

Figure 3

Efficiencies for 10×10 cm² field size, relative to the efficiency obtained for the BEAMnrc default case. The uncertainty was calculated in five different ways, i.e., using only the central bin, the bins with the minimum and maximum values, the bins with values greater than 50% of the maximum value, and, finally, considering all bins.

Figure 4

Efficiencies for the 40×40 cm² field size, relative to the efficiency obtained for the BEAMnrc default case. The uncertainty was calculated in five different ways, i.e., using only the central bin, the bins with the minimum and maximum values, the bins with values greater than 50% of the maximum value, and, finally, considering all bins.

Figure 5

Measured and calculated (BEAMnrc default parameters∕techniques) central-axis dose profiles in a water phantom for the 10×10 and 40×40 cm² field sizes. The calculations were performed with an average fractional uncertainty in the dose [for voxels with dose values greater than 50% of the maximum dose (Ref. 36)] of less than 0.01 (1%). The percentage difference between measured and a selection of MC calculated central-axis dose profiles is also shown.

Figure 6

Measured and MC calculated (BEAMnrc default parameters∕techniques) off-axis dose profiles in a water phantom for the 10×10 and 40×40 cm² field sizes. The calculations were performed with an average fractional uncertainty in the dose [for voxels with dose values greater than 50% of the maximum dose (Ref. 36)] of less than 0.01 (1%). The percentage difference, in the central region of the field and at different depths, between measured and a selection of MC calculated off-axis dose profiles is also shown.

Figure 7

Central-axis dose profiles for BEAMnrc with BH (default) and with NIST bremsstrahlung cross sections in a water phantom with a 5 cm air gap and for the 10×10 and 40×40 cm² field sizes. The calculations were performed with an average fractional uncertainty in the dose [for voxels with dose values greater than 50% of the maximum dose (Ref. 36)] of less than 0.01 (1%). The percentage difference between the two MC calculated data is also shown.

Figure 8

Off-axis dose profiles for BEAMnrc with BH (default) and with NIST bremsstrahlung cross sections in a water phantom with a 5 cm air gap and for the 10×10 and 40×40 cm² field sizes. The calculations were performed with an average fractional uncertainty in the dose [for voxels with dose values greater than 50% of the maximum dose (Ref. 36)] of less than 0.01 (1%). The percentage difference, in the central region of the field and at different depths, between the two MC calculated data is also shown.