Isothermal microcalorimetry to investigate non specific interactions in biophysical chemistry
- PMID: 20111693
- PMCID: PMC2812836
- DOI: 10.3390/ijms10083283
Isothermal microcalorimetry to investigate non specific interactions in biophysical chemistry
Abstract
Isothermal titration microcalorimetry (ITC) is mostly used to investigate the thermodynamics of "specific" host-guest interactions in biology as well as in supramolecular chemistry. The aim of this review is to demonstrate that ITC can also provide useful information about non-specific interactions, like electrostatic or hydrophobic interactions. More attention will be given in the use of ITC to investigate polyelectrolyte-polyelectrolyte (in particular DNA-polycation), polyelectrolyte-protein as well as protein-lipid interactions. We will emphasize that in most cases these "non specific" interactions, as their definition will indicate, are favoured or even driven by an increase in the entropy of the system. The origin of this entropy increase will be discussed for some particular systems. We will also show that in many cases entropy-enthalpy compensation phenomena occur.
Keywords: isothermal titration calorimetry; non-specific interactions.
Figures

interactions between α-cyclodextrins and organic guests.
interactions between catalytic antibodies and organic substrates.
interactions between albumins and organic guests.
interactions between catalytic antibodies and inhibitors.
interactions between enzymes and inhibitors.
interactions between antibodies and proteins.

 ):
, (
):
, (
 ):
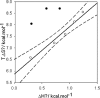
, (▪):
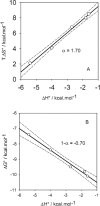
The dashed line corresponds to a process implying no change in energy.
):
, (▪):
The dashed line corresponds to a process implying no change in energy.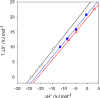
 ): I−, the slope of the linear regression is α=0.98, (
): I−, the slope of the linear regression is α=0.98, (
 ): Br−, α=0.93, (
): Br−, α=0.93, (
 ): Cl−, α=0.93. The ITC experiments were performed between 303 and 333 K. Data taken from Ref. [65].
): Cl−, α=0.93. The ITC experiments were performed between 303 and 333 K. Data taken from Ref. [65].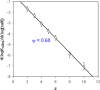

 )
-pUC118 binding and: (•) condensation of pUC118. The full and dashed lines correspond to the linear regression and the limit of the 95 % confidence interval respectively.
)
-pUC118 binding and: (•) condensation of pUC118. The full and dashed lines correspond to the linear regression and the limit of the 95 % confidence interval respectively.

Similar articles
-
Direct determination of the thermodynamics of polyelectrolyte complexation and implications thereof for electrostatic layer-by-layer assembly of multilayer films.Langmuir. 2006 Jul 4;22(14):6093-101. doi: 10.1021/la0518391. Langmuir. 2006. PMID: 16800664
-
Isothermal Titration Calorimetry.Methods Mol Biol. 2021;2263:135-159. doi: 10.1007/978-1-0716-1197-5_5. Methods Mol Biol. 2021. PMID: 33877596
-
Isothermal titration calorimetry for chiral chemistry.Chirality. 2018 May;30(5):619-631. doi: 10.1002/chir.22842. Epub 2018 Mar 12. Chirality. 2018. PMID: 29528520 Review.
-
Relationship between the growth regime of polyelectrolyte multilayers and the polyanion/polycation complexation enthalpy.J Phys Chem B. 2006 Oct 5;110(39):19443-9. doi: 10.1021/jp062264z. J Phys Chem B. 2006. PMID: 17004803
-
Analysis of cooperativity by isothermal titration calorimetry.Int J Mol Sci. 2009 Aug 4;10(8):3457-77. doi: 10.3390/ijms10083457. Int J Mol Sci. 2009. PMID: 20111687 Free PMC article. Review.
Cited by
-
Crystal structure analysis of the biologically active drug mol-ecule riluzole and riluzolium chloride.Acta Crystallogr E Crystallogr Commun. 2019 Jul 2;75(Pt 8):1084-1089. doi: 10.1107/S2056989019009022. eCollection 2019 Aug 1. Acta Crystallogr E Crystallogr Commun. 2019. PMID: 31417770 Free PMC article.
-
The Fundamental Role of Flexibility on the Strength of Molecular Binding.Soft Matter. 2012;8(23):6385-6392. doi: 10.1039/C2SM25160D. Epub 2012 May 14. Soft Matter. 2012. PMID: 22707976 Free PMC article.
-
Isothermal titration calorimetry in nanoliter droplets with subsecond time constants.Anal Chem. 2011 Oct 15;83(20):7955-61. doi: 10.1021/ac202026a. Epub 2011 Sep 26. Anal Chem. 2011. PMID: 21913688 Free PMC article.
-
Interplay between Affinity and Valency in Effector Cell Degranulation: A Model System with Polcalcin Allergens and Human Patient-Derived IgE Antibodies.J Immunol. 2019 Oct 1;203(7):1693-1700. doi: 10.4049/jimmunol.1900509. Epub 2019 Aug 28. J Immunol. 2019. PMID: 31462504 Free PMC article.
-
A Novel Cryptic Clostridial Peptide That Kills Bacteria by a Cell Membrane Permeabilization Mechanism.Microbiol Spectr. 2022 Oct 26;10(5):e0165722. doi: 10.1128/spectrum.01657-22. Epub 2022 Sep 12. Microbiol Spectr. 2022. PMID: 36094301 Free PMC article.
References
-
- Ruben AJ, Kiso Y, Freire E. Overcomming roadblocks in lead optimization:a thermodynamic perspective. Chem. Biol. Drug Des. 2006;67:2–4. - PubMed
-
- Cantor CR, Shimmel PR.Biophysical Chemistry. Part III. The behavior of biological macromolecules W.H. Freeman and Company; New York, NY, USA: 1980. Chapter 15.
-
- Rose T.di Cera E.Thermodynamic dissection of cooperativity in ligand recognition Thermodynamics in Biology Oxford University Press; New York, NY, USA: 2000. Chapter 2.
-
- Lehn JM. Supramolecumar Chemistry. Wiley-VCH. Weinheim; Berlin, Germany: 1995.
-
- Alberts B, Bray D, Lewis J, Kaff M, Roberts K, Watson JD. Molecular Biology of the Cell. 3rd Ed. Garland Publishing Inc; New York, NY, USA: 1993.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

