A new model for force generation by skeletal muscle, incorporating work-dependent deactivation

Abstract

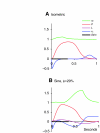
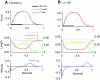
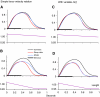
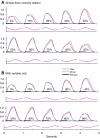
A model is developed to predict the force generated by active skeletal muscle when subjected to imposed patterns of lengthening and shortening, such as those that occur during normal movements. The model is based on data from isolated lamprey muscle and can predict the forces developed during swimming. The model consists of a set of ordinary differential equations, which are solved numerically. The model's first part is a simplified description of the kinetics of Ca(2+) release from sarcoplasmic reticulum and binding to muscle protein filaments, in response to neural activation. The second part is based on A. V. Hill's mechanical model of muscle, consisting of elastic and contractile elements in series, the latter obeying known physiological properties. The parameters of the model are determined by fitting the appropriate mathematical solutions to data recorded from isolated lamprey muscle activated under conditions of constant length or rate of change of length. The model is then used to predict the forces developed under conditions of applied sinusoidal length changes, and the results compared with corresponding data. The most significant advance of this model is the incorporation of work-dependent deactivation, whereby a muscle that has been shortening under load generates less force after the shortening ceases than otherwise expected. In addition, the stiffness in this model is not constant but increases with increasing activation. The model yields a closer prediction to data than has been obtained before, and can thus prove an important component of investigations of the neural-mechanical-environmental interactions that occur during natural movements.

Fig. 1.

Types of data collected [first published in Williams et al. (Williams et al., 1998)]. (A) Stimulation at three constant lengths. (B) Stimulation during constant-velocity shortening or lengthening. (C) Stimulation at five different phases with respect to sinusoidal movement. The phase is calculated as the time between the beginning of stimulation and the onset of shortening, as a percentage of the cycle duration. Duration of stimulus shown by horizontal bars. Forces are in mN mm⁻², lengths in mm, and time in seconds.

Fig. 2.

Behaviour of variable m during isometric (A) and sine (B) experiments. When contractile element (CE) is shortening under load, the value of m increases; otherwise, m decays to its initial value of 1. All variables are dimensionless except for time, which is in seconds. Forces (P) are given as fractions of P₀, lengths as (L—L₀)/L₀, and velocities (ν_c) as fractions of L₀ s⁻¹. Φ is delay between beginning of stimulus and beginning of shortening, as a fraction of cycle duration. See Table 1 for values of all parameters.

Fig. 3.

Effects of non-constant μ on the variables of the Hill (Hill, 1938) model. In both cases the variable m is included in the computation. (A) μ=μ₀+μ₁ throughout. (B) μ=μ₀+μ₁Caf. Axis units as in Fig. 2 except for lengths, which are given as L/L₀. In the length plots of both A and B, l_c and L are plotted on left axis, L_s (length of SE) on right axis, on same scale but with different origin.

Fig. 4.

Effect of work-dependent deactivation (WDD) on model behaviour. (A and B) Ramp data fit with parameter α_m only. (C and D) Ramp data fit with parameters α_m, k_m1 and k_m2. Isometric data recorded at the long length, from which shortening ramps begin. The red traces show the data obtained during shortening ramps at 0.33 L₀ s⁻¹ (A and C) and 0.78 L₀ s⁻¹ (B and D) and the blue traces show the model behaviour at the same ramp speeds. Length during ramps shown in bottom trace of each panel. Axis units as in Fig. 3.

Fig. 5.

Prediction of sine data. (A) Model includes only parameters α_m and α_p in the fitting of ramp data. (B) Model also includes variable m and parameters k_m1 and k_m2, as described in text. Axis units as in Fig. 3.

Fig. 6.

Work done by muscle during swimming. (A) Time course of generated force (P), rate of change of length (v_c) of contractile element (CE), and their negative cumulative product, work, for three different phases, which encompass those occurring during lamprey swimming. (B) Comparison of work predicted by model with that calculated from the experimental data at all phases.