Timing robustness in the budding and fission yeast cell cycles

Abstract

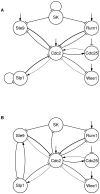
Robustness of biological models has emerged as an important principle in systems biology. Many past analyses of Boolean models update all pending changes in signals simultaneously (i.e., synchronously), making it impossible to consider robustness to variations in timing that result from noise and different environmental conditions. We checked previously published mathematical models of the cell cycles of budding and fission yeast for robustness to timing variations by constructing Boolean models and analyzing them using model-checking software for the property of speed independence. Surprisingly, the models are nearly, but not totally, speed-independent. In some cases, examination of timing problems discovered in the analysis exposes apparent inaccuracies in the model. Biologically justified revisions to the model eliminate the timing problems. Furthermore, in silico random mutations in the regulatory interactions of a speed-independent Boolean model are shown to be unlikely to preserve speed independence, even in models that are otherwise functional, providing evidence for selection pressure to maintain timing robustness. Multiple cell cycle models exhibit strong robustness to timing variation, apparently due to evolutionary pressure. Thus, timing robustness can be a basis for generating testable hypotheses and can focus attention on aspects of a model that may need refinement.

Figure 1. Budding yeast models.

Nodes in the graph represent molecules, complexes, etc. Arrows with pointed heads represent activation, and arrows with bars indicate inhibition. Thin arrows represent a weight of 1/3, normal arrows represent a weight of 1 and thick arrows represent weight 3. (A) The model from Li, et al. . (B) A subset of the model that highlights the first timing hazard. Nodes with values marked with * are enabled to change. If Cdc20 transitions from 1 to 0 before Cdh1 transitions from 0 to 1, Cdh1 will stay at 0, causing the cell cycle to arrest before it has returned to G1. (C) The hazard can be eliminated by replacing Cdc20 self-degradation with inhibition of Cdc20 by Cdh1, ensuring that Cdh1 transitions to 1 before Cdc20 transitions to 0. (D) The final speed-independent model for budding yeast.

Figure 2. Fission yeast models.

(A) Fission yeast model derived from Sveiczer, et al, 2004 . (B) Revised speed-independent model.