Vortex interactions with flapping wings and fins can be unpredictable

Abstract

As they fly or swim, many animals generate a wake of vortices with their flapping fins and wings that reveals the dynamics of their locomotion. Previous studies have shown that the dynamic interaction of vortices in the wake with fins and wings can increase propulsive force. Here, we explore whether the dynamics of the vortex interactions could affect the predictability of propulsive forces. We studied the dynamics of the interactions between a symmetrically and periodically pitching and heaving foil and the vortices in its wake, in a soap-film tunnel. The phase-locked movie sequences reveal that abundant chaotic vortex-wake interactions occur at high Strouhal numbers. These high numbers are representative for the fins and wings of near-hovering animals. The chaotic wake limits the forecast horizon of the corresponding force and moment integrals. By contrast, we find periodic vortex wakes with an unlimited forecast horizon for the lower Strouhal numbers (0.2-0.4) at which many animals cruise. These findings suggest that swimming and flying animals could control the predictability of vortex-wake interactions, and the corresponding propulsive forces with their fins and wings.

Figure 1.

Phase-locked averages wake images reveal abundant chaotic vortex-wake interactions as a function of flapping foil kinematics; dimensionless heave amplitude A* and wavelength λ*, and pitch amplitude α₀, which are illustrated in (a). (a) A* = 1; (b) A* = 2. Empty spaces represent α_eff < 0° (no thrust) for which we made no measurements. White lines (dashed) indicate the borderline between chaotic and periodic flow according to λ* = 2π × A*/tan(50° + α₀/4) (see text for definition). The blue bar under the figure indicates the range of λ* at which swimming and flying animals are known to cruise for the corresponding A* (which together build up the corresponding Strouhal number range).

Figure 2.

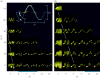
(a) Phase-locked averages wake images for A* = 3 (figure 1). (b) Pooled normalized standard deviation of I₀, I_1,r and I_2,r (with respect to maximum value) as a function of α_ind at constant α₀ shows approximately exponential growth. Exponential fits from left to right for pooled I yield (α₀ = 0°; r² = 0.95); (α₀ = 15°; r² = 0.94); (α₀ = 30°; r² = 0.92); (α₀ = 45°; r² = 0.97); (α₀ = 60°; r² = 0.91). (c) Standard deviation of I₀ (outer circle), I_1,r (middle circle), and I_2,r, (inner circle) plotted as a function of α_eff and α_ind, which are colour-coded from minimum to maximum/2; (0.4c)² ≤ s(I₀) ≤ (2.6c)²; (1.2c)³ ≤ s(I_1,r) ≤ (4.1c)³; (2.1c)⁴ ≤ s(I_2,r) ≤ (5.6c)⁴. We find a periodic vortex-wake domain at low values of α_ind (which corresponds with Strouhal number) and a chaotic domain at high values (yellow area). The border between both domains can be described by α_eff = 247° − 3.15α_ind and represents the left border of the yellow area (crosses indicated the calculated intersections in (b) to which the borderline is fitted). Animals preferably cruise at low Strouhal numbers St, in the range 0.2–0.4 (Taylor et al. 2003), for which we find solely periodic vortex-wake interactions.