Validation of a fluid-structure interaction model of solute transport in pores of cyclically deformed tissue scaffolds

Abstract

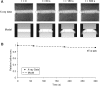
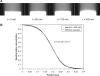
Convection induced by repetitive compression of porous tissue scaffolds enhances solute transport inside the scaffold. Our previous experiments have shown that pore size, shape, and orientation with respect to strain direction greatly influence loading-induced solute transport. The objective of this study was to develop a computational model of deformation-induced solute transport in porous tissue scaffolds, which included the pore geometry of the scaffold. This geometry consisted of a cubic scaffold with single channel in the middle of the scaffold, immersed in a fluid reservoir. Cylindrical pores with circular or elliptic cross section, and spheroid pores were modeled. The scaffold was cyclically compressed from one side, causing fluid motion and dispersion of solute inside the scaffold pore. Scaffold deformation was solved using the finite element method, and fluid flow and solute transport were solved using the finite volume method. The distortion of the scaffold-fluid interface was transferred as a boundary condition to the fluid flow solver. Both convection and diffusion were included in the computations. The solute transport rates in the different scaffold pore geometries agreed well with our previous experimental results obtained with X-ray microimaging. This model will be used to explore transport properties of a spectrum of novel scaffold designs.

FIG. 1.

Schematic diagram of the model. (A) A deformable scaffold is immersed in a fluid reservoir underneath a compression device. The pore of the scaffold is initially filled with contrast agent. Cycles of (B) compression and (C) release are applied to the scaffold, inducing a convective fluid flow in the scaffold pore, thereby transporting the tracer from the pore into the surrounding fluid reservoir.

FIG. 2.

The modeled scaffold pore geometries. (A) Circular cylinder with channel diameter d₁. (B) Elliptic cylinder with minor axis d₁ and major axis d₂. (C) Spheroid pore with opening diameter d₁ and maximum diameter d₂. See Table 1 for dimensions.

FIG. 3.

Discretization of the solid and fluid domains for numerical solution of the model partial differential equations using the finite element and finite volume methods. (A) Solid mesh and (B) fluid mesh (pore + reservoir) of a scaffold with 1.38 mm circular cylindrical pore. (C) Solid mesh and (D) fluid mesh of a scaffold with spheroid pore.

FIG. 4.

Schematic diagram of the boundary conditions used in the model.

FIG. 5.

X-ray data and computational fluid dynamics model results compared during passive (gravitation induced) removal of contrast agent from the scaffold channel. (A) Distribution of contrast agent inside the channel. (B) Average concentration of iodine in the channel.

FIG. 6.

X-ray data and computational fluid dynamics model results compared during compression-induced removal of contrast agent from the scaffold channel. (A) Circular cylinder. (B) Elliptic cylinder with minor axis in the strain direction. (C) Spheroid.

FIG. 7.

Model-predicted relative iodine concentration in (A) the elliptical channels and (B) the spheroid and circular channels compared to the X-ray data. The error bars result from n = 5 repeated experiments. (C) Percentage of iodine removed as predicted by the computational model compared to X-ray data for the different channel shapes at t = 100 s. Notice the excellent agreement between model and data.

FIG. 8.

Model predicted distribution of solute at t = 100 s inside a scaffold with interconnected circular channels (d = 1.0 mm) upon compression-induced cyclic deformation with 15% strain at 1.0 Hz.

FIG. A1.

(A) X-ray projection images of diffusion of sodium iodide in glycerol at different time points. The glycerol is dark and the iodine is light. (B) Fit of the analytical diffusion equation to calculate the diffusion coefficient.