Dynamic infant-parent affect coupling during the face-to-face/still-face

Abstract

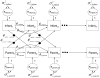
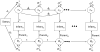
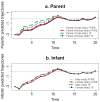
We examined dynamic infant-parent affect coupling using the Face-to-Face/Still-Face (FFSF). The sample included 20 infants whose older siblings had been diagnosed with Autism Spectrum Disorders (ASD-sibs) and 18 infants with comparison siblings (COMP-sibs). A series of mixed effects bivariate autoregressive models was used to represent the self-regulation and interactive dynamics of infants and parents during the FFSF. Significant bidirectional affective coupling was found between infants and parents, with infant-to-parent coupling being more prominent than parent-to-infant coupling. Further analysis of within-dyad dynamics revealed ongoing changes in concurrent infant-parent linkages both within and between different FFSF episodes. The importance of considering both inter- and intradyad differences is discussed.

Figure 1

Screenshot of the Continuous Measurement System (CMS).

Figure 2

(a), (c) & (d): Plots of each infant’s mean ratings during the FF, SF and RE, respectively; (b), (d) & (e): plots of each parent’s mean ratings during FF, SF and RE.

Figure 3

Path diagram of the bivariate AR(2) model. The dark filled circles attached to the lag-1 cross-regression paths, φ_{infant–>parent,i} and φ_{parent–>infant,i} indicate that individual differences are included in the P→I and I→P cross-regression parameters. The index for episode (k) is omitted from the path diagram to simplify the notations. Infant_it = manifest measurement of infant (in dyad) i’s emotional valence at time t; Parent_it = manifest measurement of parent (in dyad) i’s emotional valence at time t e_infant,it = measurement error for infant; e_parent,it = measurement error for parent; ${\sigma }_{e,\mathit{infant}}^2$ = measurement error variance for infant; ${\sigma }_{e,\mathit{parent}}^2$ = measurement error variance for parent; φ_1,infant, φ_{1, parent}, φ_2,infant, φ_{2, parent} = AR(1) parameter for infant, AR(1) parameter for parent, AR(2) parameter for infant and AR(2) parameter for parent; φ_{infant–>parent} = cross-regression from infant’s emotion at time t−1 to parent’s emotion at time t; φ_{parent–>infant} = cross-regression from parent’s emotion at time t−1 to infant’s emotion at time t.

Figure 4

Path diagram of the stochastic regression model with AR(2) component used to represent time-varying concurrent synchrony between parents and infants. The index for episode (k) is omitted from the path diagram to simplify the notations. Infant_it = manifest measurement of infant (in dyad) i’s emotional valence at time t; Parent_it = manifest measurement of parent (in dyad) i’s emotional valence at time t; Status_i = ASD status for infant i (0 for COMP-sibs, 1 for ASD-sibs); α_it = AR component; φ₁ =AR(1) parameter; φ₂ =AR(2) parameter; B_it = regression parameter at time t; ${\sigma }_{{\alpha }_0}^2$ = variance for AR component; ${\sigma }_{B_0}^2$ = variance for time-varying regression parameter; d₁ = deviation in AR variance associated with ASD-sibs compared with COMP-sibs; d₂ = deviation in variance for the regression parameter associated with ASD-sibs compared with COMP-sibs.

Figure 5

(a) Predicted trajectories of parents of male vs. female infants in the SF vs. FF/RE condition; (b) Predicted trajectories of male and female infants in the SF vs. FF/RE condition. The horizontal dotted lines in (a) and (b) represent the baseline affective level toward which each participant’s recovery trajectory converges. One time series of residual errors, e_t, is used in all simulations to generate the same magnitudes of perturbations in all conditions. For infants, the predicted trajectories are generated by iterating through the equation $${\mathit{Infant}}_{\mathit{ikt}}=1.16{\mathit{Infant}}_{ik,t-1}-.36{\mathit{Infant}}_{ik,t-2}+(.03-.02\mathit{SFvsFF}/R{E}_{ik}){\mathit{Parent}}_{ik,t-1}+e_t,$$ whereas the predicted trajectories for parents are generated using the same initial condition and time series of residual errors, but with $${\mathit{Parent}}_{\mathit{ikt}}=.98{\mathit{Parent}}_{ik,t-1}-.20{\mathit{Parent}}_{ik,t-2}+[.05+.002{\mathit{Gender}}_i-.05\mathit{SFvsFF}/R{E}_{ik}]+.02({\mathit{Gender}}_i\times \mathit{SFvsFF}/R{E}_{ik})]{\mathit{Infant}}_{ik,t-1}+e_t.$$

Figure 6

Estimated regression weights for each dyad based on parameter estimates from the final AR with stochastic regression model. The regression weights were estimated by means of the Kalman smoother for (a) the FF episode, (b) the SF episode and (c) the RE episode.