Electrostatic solvation energy for two oppositely charged ions in a solvated protein system: salt bridges can stabilize proteins

Abstract

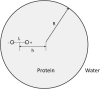
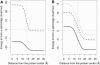
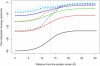
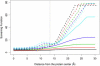
Born-type electrostatic continuum methods have been an indispensable ingredient in a variety of implicit-solvent methods that reduce computational effort by orders of magnitude compared to explicit-solvent MD simulations and thus enable treatment using larger systems and/or longer times. An analysis of the limitations and failures of the Born approaches serves as a guide for fundamental improvements without diminishing the importance of prior works. One of the major limitations of the Born theory is the lack of a liquidlike description of the response of solvent dipoles to the electrostatic field of the solute and the changes therein, a feature contained in the continuum Langevin-Debye (LD) model applied here to investigate how Coulombic interactions depend on the location of charges relative to the protein/water boundary. This physically more realistic LD model is applied to study the stability of salt bridges. When compared head to head using the same (independently measurable) physical parameters (radii, dielectric constants, etc.), the LD model is in good agreement with observations, whereas the Born model is grossly in error. Our calculations also suggest that a salt bridge on the protein's surface can be stabilizing when the charge separation is < or =4 A.

Figure 1

Geometrical description of the model biological system. A spherical protein of radius R is placed in water. A pair of oppositely charged ions, separated by a distance L, is placed along a radial line with the center of the dipole situated at a distance h from the center of the protein.

Figure 2

Comparison of solvation and transfer free energies between the LD model (solid line) and the Born model (dashed line). (A) The electrostatic solvation energy calculated for a dipole composed of two unit charges of opposite sign and with a fixed length of 3 Å placed at various positions in the protein-water system. (B) The transfer free energy required to move the dipole from water into the interior of the protein, calculated by subtracting the baseline from the two curves in A. The protein is spherical, with a radius of 13.4 Å, which corresponds to the radius of gyration of a 100-residue globular protein. The dotted vertical line denotes the position of the boundary between the spherical protein and water.

Figure 3

Free energy of formation of a salt bridge between a pair of oppositely charged unit charges in the protein/water system. (A) The energy for a dipole with an intercharge separation of 3 Å as calculated using the LD (solid line) and Born models (dashed line). (B) The energy profiles for ion pairs at larger intercharge separations for the LD model: 4 Å (solid line), 5 Å (dashed line); and 6 Å (dotted line). The vertical thin dotted lines in both graphs represent the location of the boundary between the protein and water. The horizontal thin dotted lines represent an energy of 0 kcal/mol, so the points beneath this line correspond to situations that stabilize protein folding.

Figure 4

Electrostatic interaction energy for a pair of opposite unit charges as calculated from the LD (solid lines) and Born models (dashed lines). The ion pair separations are 3 Å (black), 4 Å (red), 5 Å (green), 6 Å (blue), and 7 Å (cyan).

Figure 5

Screening function for a pair of opposite unit charges as calculated from the LD (solid lines) and Born models (dashed lines). The ion pair separations are 3 Å (black), 4 Å (red), 5 Å (green), 6 Å (blue), and 7 Å (cyan).