Human strategy updating in evolutionary games

Abstract

Evolutionary game dynamics describe not only frequency-dependent genetic evolution, but also cultural evolution in humans. In this context, successful strategies spread by imitation. It has been shown that the details of strategy update rules can have a crucial impact on evolutionary dynamics in theoretical models and, for example, can significantly alter the level of cooperation in social dilemmas. What kind of strategy update rules can describe imitation dynamics in humans? Here, we present a way to measure such strategy update rules in a behavioral experiment. We use a setting in which individuals are virtually arranged on a spatial lattice. This produces a large number of different strategic situations from which we can assess strategy updating. Most importantly, spontaneous strategy changes corresponding to mutations or exploration behavior are more frequent than assumed in many models. Our experimental approach to measure properties of the update mechanisms used in theoretical models will be useful for mathematical models of cultural evolution.

Fig. 1.

Strategy updating in behavioral experiments with fixed neighbors. Most strategy changes can be explained by imitation of the most successful neighbor (full bars), that is, changing to the best available strategy in a heterogeneous environment in which neighbors play different strategies (brown) or sticking to the strategy when everyone does the same in a homogeneous environment (orange). However, a large portion of strategy changes cannot be explained by imitation (open bars). These changes represent either spontaneous strategy switching in homogeneous environments with no role model (open orange bars) or choosing a strategy that did not perform best in an environment with different neighboring strategies (open brown bars). The line shows a fit of the fraction of strategy changes not explained by imitation. This fraction decays approximately exponentially as ν₀·Γ^{t −1}. Nonlinear regression leads to ν₀ = 0.380 ± 0.013 and Γ = 0.962 ± 0.003 (full line). The diagrams on the right show an example for a heterogeneous environment (Upper) and a homogeneous environment (Lower) of a focal cooperating player. In total, we have 4,315 heterogeneous situations and 1,445 homogeneous situations in our 5,760 strategy choice situations (graphic shows averages over 15 fixed-neighbor treatments with 25 rounds and 16 players each).

Fig. 2.

The average level of cooperation tends to decrease over time. Symbols show a behavioral experiment with humans, and lines correspond to simulations. In the experiment, the treatment with fixed neighbors on a 4 × 4 lattice with periodical boundary conditions (▪) is not significantly different from the dynamics in a system with random neighbors (▲). Full lines show a computer simulation in which players either imitate their best-performing neighbor or choose a random strategy with a probability of 2ν·Γ^{t −1}, where ν = 0.38 and Γ = 0.96 (fitted to the behavioral experiment; see the text). For such a high probability of random strategy choice, the simulation results for fixed and random neighbors are almost indistinguishable and the level of cooperation is driven by random strategy choice rather than by spatial structure. For comparison, dotted lines show computer simulations with no mutations (experimental average over 15 repeats for fixed neighbors and 10 repeats for random neighbors, each with 16 players; simulations starting from the cooperation level of the experiment and averaged over 10⁴ realizations).

Fig. 3.

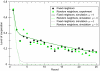
Strategy updating in a spatial game. (A) As expected, the probability of switching to another strategy increases with the payoff difference. Theoretical models typically assume strategy update functions such as, for example, , where P is the probability of switching strategy and Δπ is the payoff difference. Fitting this function leads to an intensity of selection β = 1.20 ± 0.25 (solid line). However, the data for cooperating and defecting players seem to follow different characteristics, and defecting players seem to be more resilient to change than cooperators. To capture this, we have also fitted the two different data sets to the function (dotted lines). This approach leads to β_C = 0.67 ± 0.28 and α_C = −0.11 ± 0.23 for cooperating players. For defecting players, we find β_D = 0.99 ± 0.23 and α_D = 0.79 ± 0.14. (Inset) Probability of changing strategies spontaneously, without any role models playing a different strategy. Such spontaneous changes correspond to mutations and occur with a probability of 0.28 ± 0.07 (cooperating players switching to defection) or 0.25 ± 0.01 (defecting players switching to cooperation). This probability is much higher in our experiment than typically assumed for theoretical models but decreases exponentially in time (Fig. 1). (B) Another perspective is to infer the probability of cooperating in the next round, given the number of cooperating neighbors in the current round. This probability is highest if all neighbors cooperate, although, in this case, the payoff from defection would be highest. This indicates that humans do not only imitate what is successful but what is common (all error bars are the SDs of a binomial distribution, , where n is the number of samples).