Using simple artificial intelligence methods for predicting amyloidogenesis in antibodies
- PMID: 20144194
- PMCID: PMC3098112
- DOI: 10.1186/1471-2105-11-79
Using simple artificial intelligence methods for predicting amyloidogenesis in antibodies
Abstract
Background: All polypeptide backbones have the potential to form amyloid fibrils, which are associated with a number of degenerative disorders. However, the likelihood that amyloidosis would actually occur under physiological conditions depends largely on the amino acid composition of a protein. We explore using a naive Bayesian classifier and a weighted decision tree for predicting the amyloidogenicity of immunoglobulin sequences.
Results: The average accuracy based on leave-one-out (LOO) cross validation of a Bayesian classifier generated from 143 amyloidogenic sequences is 60.84%. This is consistent with the average accuracy of 61.15% for a holdout test set comprised of 103 AM and 28 non-amyloidogenic sequences. The LOO cross validation accuracy increases to 81.08% when the training set is augmented by the holdout test set. In comparison, the average classification accuracy for the holdout test set obtained using a decision tree is 78.64%. Non-amyloidogenic sequences are predicted with average LOO cross validation accuracies between 74.05% and 77.24% using the Bayesian classifier, depending on the training set size. The accuracy for the holdout test set was 89%. For the decision tree, the non-amyloidogenic prediction accuracy is 75.00%.
Conclusions: This exploratory study indicates that both classification methods may be promising in providing straightforward predictions on the amyloidogenicity of a sequence. Nevertheless, the number of available sequences that satisfy the premises of this study are limited, and are consequently smaller than the ideal training set size. Increasing the size of the training set clearly increases the accuracy, and the expansion of the training set to include not only more derivatives, but more alignments, would make the method more sound. The accuracy of the classifiers may also be improved when additional factors, such as structural and physico-chemical data, are considered. The development of this type of classifier has significant applications in evaluating engineered antibodies, and may be adapted for evaluating engineered proteins in general.
Figures

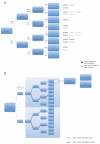


Similar articles
-
Prediction and analysis of antibody amyloidogenesis from sequences.PLoS One. 2013;8(1):e53235. doi: 10.1371/journal.pone.0053235. Epub 2013 Jan 7. PLoS One. 2013. PMID: 23308169 Free PMC article.
-
SCPRED: accurate prediction of protein structural class for sequences of twilight-zone similarity with predicting sequences.BMC Bioinformatics. 2008 May 1;9:226. doi: 10.1186/1471-2105-9-226. BMC Bioinformatics. 2008. PMID: 18452616 Free PMC article.
-
Accuracy of structure-based sequence alignment of automatic methods.BMC Bioinformatics. 2007 Sep 20;8:355. doi: 10.1186/1471-2105-8-355. BMC Bioinformatics. 2007. PMID: 17883866 Free PMC article.
-
Recognition of protein function using the local similarity.J Bioinform Comput Biol. 2008 Aug;6(4):709-25. doi: 10.1142/s021972000800359x. J Bioinform Comput Biol. 2008. PMID: 18763738
-
FISH Amyloid - a new method for finding amyloidogenic segments in proteins based on site specific co-occurrence of aminoacids.BMC Bioinformatics. 2014 Feb 24;15:54. doi: 10.1186/1471-2105-15-54. BMC Bioinformatics. 2014. PMID: 24564523 Free PMC article.
Cited by
-
AB-Amy: machine learning aided amyloidogenic risk prediction of therapeutic antibody light chains.Antib Ther. 2023 Apr 12;6(3):147-156. doi: 10.1093/abt/tbad007. eCollection 2023 Jul. Antib Ther. 2023. PMID: 37492587 Free PMC article.
-
Machine learning methods can replace 3D profile method in classification of amyloidogenic hexapeptides.BMC Bioinformatics. 2013 Jan 17;14:21. doi: 10.1186/1471-2105-14-21. BMC Bioinformatics. 2013. PMID: 23327628 Free PMC article.
-
MetAmyl: a METa-predictor for AMYLoid proteins.PLoS One. 2013 Nov 19;8(11):e79722. doi: 10.1371/journal.pone.0079722. eCollection 2013. PLoS One. 2013. PMID: 24260292 Free PMC article.
-
Computer-aided antibody design.Protein Eng Des Sel. 2012 Oct;25(10):507-21. doi: 10.1093/protein/gzs024. Epub 2012 Jun 2. Protein Eng Des Sel. 2012. PMID: 22661385 Free PMC article. Review.
-
Categorization of 77 dystrophin exons into 5 groups by a decision tree using indexes of splicing regulatory factors as decision markers.BMC Genet. 2012 Mar 31;13:23. doi: 10.1186/1471-2156-13-23. BMC Genet. 2012. PMID: 22462762 Free PMC article.
References
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

