Identification of intraday metabolic profiles during closed-loop glucose control in individuals with type 1 diabetes

Abstract

Background: Algorithms for closed-loop insulin delivery can be designed and tuned empirically; however, a metabolic model that is predictive of clinical study results can potentially accelerate the process.

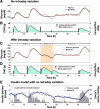
Methods: Using data from a previously conducted closed-loop insulin delivery study, existing models of meal carbohydrate appearance, insulin pharmacokinetics, and the effect on glucose metabolism were identified for each of the 10 subjects studied. Insulin's effects to increase glucose uptake and decrease endogenous glucose production were described by the Bergman minimal model, and compartmental models were used to describe the pharmacokinetics of subcutaneous insulin absorption and glucose appearance following meals. The composite model, comprised of only five equations and eight parameters, was identified with and without intraday variance in insulin sensitivity (S(I)), glucose effectiveness at zero insulin (GEZI), and endogenous glucose production (EGP) at zero insulin.

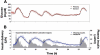
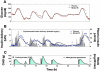
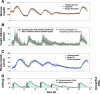
Results: Substantial intraday variation in SI, GEZI and EGP was observed in 7 of 10 subjects (root mean square error in model fit greater than 25 mg/dl with fixed parameters and nadir and/or peak glucose levels differing more than 25 mg/dl from model predictions). With intraday variation in these three parameters, plasma glucose and insulin were well fit by the model (R(2) = 0.933 +/- 0.00971 [mean +/- standard error of the mean] ranging from 0.879-0.974 for glucose; R(2) = 0.879 +/- 0.0151, range 0.819-0.972 for insulin). Once subject parameters were identified, the original study could be reconstructed using only the initial glucose value and basal insulin rate at the time closed loop was initiated together with meal carbohydrate information (glucose, R(2) = 0.900 +/- 0.015; insulin delivery, R(2) = 0.640 +/- 0.034; and insulin concentration, R(2) = 0.717 +/- 0.041).

Conclusion: Metabolic models used in developing and comparing closed-loop insulin delivery algorithms will need to explicitly describe intraday variation in metabolic parameters, but the model itself need not be comprised by a large number of compartments or differential equations.

Figure 1.

Average profile of all 10 subjects. (A) Closed-loop plasma glucose (closed circles ± standard error) and sensor (solid curve; SEM not shown) observed in the adults studied under closed-loop PID insulin delivery. (B) Plasma insulin concentrations (closed circles ± standard error) and fitted PK insulin model (solid curve; SEM not shown) using the experimentally obtained insulin delivery profile (shaded area) as input to Equation (1). Profiles were fit individually and then averaged.

Figure 2.

Identification of a subject where no intraday variation was necessary to fit the glucose profile (subject 7). (A) Plasma glucose concentration (solid circles) and model fit (solid curve) showing peak postprandial and nadir glucose for glucose below 80 mg/dl within 15 mg/dl and each occurring with 0.5 h of each other. (B) Proportional-integral-derivative insulin delivery profile (shaded region) and measured insulin concentration5 (solid circles) with model insulin profile (solid curve). (C) Carbohydrates intake (bars, left axis) with model [Equation (5)] estimated exogenous glucose appearance (solid curve with shading, right axis).

Figure 3.

Identification of a subject where intraday variation in model parameters was necessary to adequately fit plasma glucose (subject 8). (A) Glucose profile fit without intraday variation. (B) Meal glucose appearance identified without intraday variance. (C) Glucose profile fit with an increase in insulin sensitivity (S_I) and decrease in endogenous glucose production (EGP) during window 2. (D) Meal glucose appearance identified with intraday variance. (E) Proportional-integral-derivative insulin delivery profile (shaded region) and measured insulin concentration (solid circles) obtained from the original study data together with the fitted plasma insulin profile (solid curve).

Figure 4.

Average fit (solid curve) and simulated (dashed curve) profiles of all 10 subjects. Profiles were fit and simulated individually and then averaged. (A) Plasma glucose (circles ± standard error), model fit (solid curve; standard error bars not shown) using measured plasma insulin concentrations, and closed-loop model simulation (dashed curve; standard error bars not shown) results. (B) Insulin delivery obtained from the original closed-loop study with shaded area indicating the 95% confidence interval for the mean, together with the simulated profile (solid curve; standard error bars not shown) using the MVP model [Equations (1)–(5)] and PID algorithm. (C) Plasma insulin (circles ± standard error) obtained in the original study with model fit using the measured insulin delivery (solid curve; standard error not shown) and simulated values using only the initial conditions at the time closed loop was started (dashed curve; standard error not shown).