Near-isometric flattening of brain surfaces

Abstract

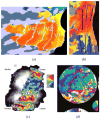
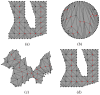
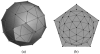
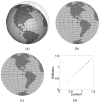
Flattened representations of brain surfaces are often used to visualize and analyze spatial patterns of structural organization and functional activity. Here, we present a set of rigorous criteria and accompanying test cases with which to evaluate flattening algorithms that attempt to preserve shortest-path distances on the original surface. We also introduce a novel flattening algorithm that is the first to satisfy all of these criteria and demonstrate its ability to produce accurate flat maps of human and macaque visual cortex. Using this algorithm, we have recently obtained results showing a remarkable, unexpected degree of consistency in the shape and topographic structure of visual cortical areas within humans and macaques, as well as between these two species.

Figure 1

Flat maps of human visual cortex from the studies of (a) Bles et al. (2006), (b) Slotnick and Yantis (2003), (c) Wandell (1999), and (d) Schira et al. (2007). The flattening procedure in BrainVoyager (Goebel, 2000) was used to produce (a) and (b), whereas (c) and (d) were produced by the flattening procedure in MrVista (Wandell et al., 2000). Although these figures suggest considerable inter-subject variability in the shape and topographic structure of V1 and V2, it is likely that much of this variability is due to the flattening procedures (see text). The stereotyped shape of human and macaque V1 is discussed in Hinds et al. (2008); see also Figure 11 and Figure 12.

Figure 2

(a) The shortest path between two points on a flat, non-convex surface is shown in black. Any flattening algorithm that takes this surface as input and attempts to match the length of the shortest path shown in (a) to the length of the corresponding straight-line path on the “flattened” output (b) will inevitably distort the input surface, violating criterion C1. (The flat map shown in (b) was generated by the Schwartz89 algorithm described in Schwartz et al., 1989.)

Figure 3

(a) A piecewise-flat surface with a pentagonal boundary and vertices uniformly spaced on the unit sphere. (b) The Schwartz89 algorithm produces a flat map of this surface with several edge-crossings (e.g., see arrow) due to folds, violating criterion C4.

Figure 4

(a) A triangular mesh of a cube, minus the bottom (square) face. The front face is colored red for reference only. (b) A non-uniform refinement of (a), resulting in a different mesh representing the same surface. (c) The flat map of (a) produced by the Schwartz89 algorithm. Applying the same algorithm to (b) results in a very different flat map, shown in (d).

Figure 5

(a) A flat, non-convex mesh was chosen as the test case for criterion C1. (b) The result of mapping (a) to a disk via Tutte's algorithm (Tutte, 1963). This provides an initial flat map (with error E = 65.9%) that is used as the starting point for the optimization routine in the DMflatten algorithm. (c) After 10 iterations of the DMflatten optimization routine, E is reduced to 27.6%. (d) The algorithm terminates after 1291 iterations, taking less than a second on a workstation with a 3 GHz processor and 2 GB of memory. The final flat map, for which E = 0.0%, is identical to the input mesh (a), demonstrating that the DMflatten algorithm satisfies criterion C1. (Red vertices are for reference only.)

Figure 6

To construct a test case for criterion C2, the flat, U-shaped mesh shown in Figure 5(a) was gently deformed onto a large sphere, resulting in the mesh shown in (a). Given this surface as the input, the DMflatten algorithm produces the output shown in (b), with flattening error E = 0.1%. By comparing this flat map to the one in Figure 5(d), we see that small deformations of the input to the DMflatten algorithm lead to small deformations of the output, satisfying criterion C2.

Figure 7

(a) The hemicylinder is a surface with zero Gaussian curvature. (b) The DMflatten algorithm correctly produces an isometric flattening of this surface (E = 0.0%), satisfying criterion C3.

Figure 8

Given the surface with pentagonal boundary from Figure 3 as the input (a), the DMflatten algorithm produces a flat map (b) with no edge-crossings, satisfying criterion C4. Although this flat map is optimal, it is significantly distorted (E = 33.0%), which is not surprising given the small boundary of the input surface, relative to its surface area.

Figure 9

Two different triangular meshes representing a cube (minus one face) are shown in (a) and (b). The corresponding flat maps, as computed by the DMflatten algorithm, are shown in (c) and (d), with flattening errors of 21.1% and 20.9%, respectively. Note that these two flat maps are nearly identical, demonstrating that the DMflatten algorithm produces mesh-independent flat maps (criterion C5).

Figure 10

Given the hemisphere (a) as the input, the DMflatten algorithm produces the output shown in (b). This flat map (E = 9.9%) is in close agreement with Lambert's equal area projection, which is shown in (c). In (d), Euclidean distances in the Lambert projection are plotted against the corresponding Euclidean distances in the DMflatten output, to further examine the level of agreement. These points lie almost exactly on the line y = x (R² > 0.999). These results demonstrate that the DMflatten algorithm correctly flattens spherical caps, satisfying criterion C6.

Figure 11

(a) Area V1 in macaque, reconstructed from serial tissue sections (Schwartz et al., 1988). (b) The result of applying the DMflatten algorithm to the surface shown in (a). The per-vertex error E_i is shown in color, both on the input surface and on the flat map, and the overall flattening error E is 4.2%. The time taken to flatten this mesh, which has 1237 vertices, is approximately 1 minute on a workstation with a 3 GHz processor and 2 GB of memory.

Figure 12

(a) Human V1, reconstructed from manual tracings of the stria of Gennari in ex vivo 7T MRI scans (Hinds et al., 2008). (b) The result of applying the DMflatten algorithm to the surface shown in (a). The per-vertex error E_i is shown in color, both on the input surface and on the flat map, and the overall flattening error E is 5.7%. The time taken to flatten this mesh, which has 2585 vertices, is approximately 10 minutes on a workstation with a 3 GHz processor and 2 GB of memory.