Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2009 Oct 1;50(7-8):959-974.
doi: 10.1016/j.mcm.2009.02.007.

A Mathematical Model for the First-Pass Dynamics of Antibiotics Acting on the Cardiovascular System

H T Banks  1 , Kathleen Holm, Nathan C Wanner, Ariel Cintrón-Arias, Grace M Kepler, Jeffrey D Wetherington
Affiliations

A Mathematical Model for the First-Pass Dynamics of Antibiotics Acting on the Cardiovascular System

H T Banks et al. Math Comput Model. .

Abstract

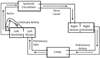
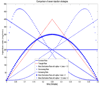
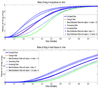
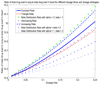
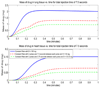
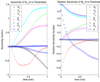
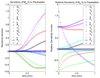
We present a preliminary first-pass dynamic model for delivery of drug compounds to the lungs and heart. We use a compartmental mass balance approach to develop a system of nonlinear differential equations for mass accumulated in the heart as a result of intravenous injection. We discuss sensitivity analysis as well as methodology for minimizing mass in the heart while maximizing mass delivered to the lungs on a first circulatory pass.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Simplification of circulatory system.
Figure 2
Figure 2
Compartment model diagram.
Figure 3
Figure 3
Absorption and metabolic rates in lung as function of MT for parameter values a = 1, b = 2, K1 = 1, K2 = 1.
Figure 4
Figure 4
Model output for parameter values found in Table 2 with varying values of D and T: D = 100, T = .5 (solid line); D = 50, T = .3 (dashed line); D = 10, T = .1 (dot-dash line).
Figure 5
Figure 5
Comparison of different injection strategies with T = .5 minutes and D = 100 mg.
Figure 6
Figure 6
Plots of MT and MH for seven different injection strategies shown in Figure 5.
Figure 7
Figure 7
Plot of the ratio of peak drug mass in the lung to peak drug mass in the heart for different dosing strategies and injection times. Injection times were sampled from .01 to .25 minutes with a step-size of .01.
Figure 8
Figure 8
Plot of the ratio of total drug load in the lung to total drug load in the heart over one minute for different dosing strategies and injection times. Injection times were sampled from .01 to .25 minutes with a step-size of .01.
Figure 9
Figure 9
Plot of constant rate injection strategy with different number of pulses and value of two ratios (peak mass of drug in lung to peak mass of drug in heart and total drug load in lung to total drug load in heart) as a function of the number of pulses.
Figure 10
Figure 10
MT and MH for constant rate injection strategy with several different pulsing strategies.
Figure 11
Figure 11
Sensitivity and relative sensitivity functions for MT (t; θ) to all parameters.
Figure 12
Figure 12
Sensitivity and relative sensitivity functions for MH(t; θ) to all parameters.
Figure 13
Figure 13
Sensitivity and relative sensitivity functions for all states to parameter d.
Figure 14
Figure 14
Iterative modeling process.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Adams D, McKinley M. The Sheep. ANZCCART News. 1995;8 Insert.
    1. Bai P, Banks HT, Dediu S, Govan AY, Last M, Lloyd AL, Nguyen HK, Olufsen MS, Rempala G, Slenning BD. Stochastic and deterministic models for agricultural production networks. Mathematical Biosciences and Engineering. 2007;4(3):373–402. - PubMed
    1. Banks HT. Lecture Notes in Biomathematics. Vol 6. Heidelberg: Springer-Verlag; 1975. Modeling and Control in the Biomedical Sciences.
    1. Banks HT, Tran HT. Mathematical and Experimental Modeling of Physical and Biological Processes. Boca Raton: CRC Press; 2009.
    1. Batzel JJ, Kappel F, Schneditz D, Tran HT. Cardiovascular and Respiratory Systems: Modeling, Analysis, and Control. Philadelphia: SIAM; 2007.

LinkOut - more resources