Micromechanical models of helical superstructures in ligament and tendon fibers predict large Poisson's ratios
- PMID: 20181336
- PMCID: PMC2881222
- DOI: 10.1016/j.jbiomech.2010.01.004
Micromechanical models of helical superstructures in ligament and tendon fibers predict large Poisson's ratios
Abstract
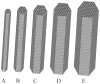
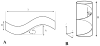
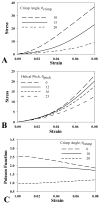
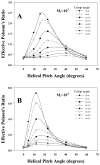
Experimental measurements of the Poisson's ratio in tendon and ligament tissue greatly exceed the isotropic limit of 0.5. This is indicative of volume loss during tensile loading. The microstructural origin of the large Poisson's ratios is unknown. It was hypothesized that a helical organization of fibrils within a fiber would result in a large Poisson's ratio in ligaments and tendons, and that this helical organization would be compatible with the crimped nature of these tissues, thus modeling their classic nonlinear stress-strain behavior. Micromechanical finite element models were constructed to represent crimped fibers with a super-helical organization, composed of fibrils embedded within a matrix material. A homogenization procedure was performed to determine both the effective Poisson's ratio and the Poisson function. The results showed that helical fibril organization within a crimped fiber was capable of simultaneously predicting large Poisson's ratios and the nonlinear stress-strain behavior seen experimentally. Parametric studies revealed that the predicted Poisson's ratio was strongly dependent on the helical pitch, crimp angle and the material coefficients. The results indicated that, for physiologically relevant parameters, the models were capable of predicting the large Poisson's ratios seen experimentally. It was concluded that helical organization within a crimped fiber can produce both the characteristic nonlinear stress-strain behavior and large Poisson's ratios, while fiber crimp alone could only account for the nonlinear stress-strain behavior.
Copyright 2010 Elsevier Ltd. All rights reserved.
Figures
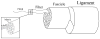

Similar articles
-
A micromechanical model of tendon and ligament with crimped fibers.J Mech Behav Biomed Mater. 2020 Dec;112:104086. doi: 10.1016/j.jmbbm.2020.104086. Epub 2020 Sep 12. J Mech Behav Biomed Mater. 2020. PMID: 32950952
-
Continuum description of the Poisson's ratio of ligament and tendon under finite deformation.J Biomech. 2014 Sep 22;47(12):3201-9. doi: 10.1016/j.jbiomech.2014.05.011. Epub 2014 May 23. J Biomech. 2014. PMID: 25134434 Free PMC article.
-
Micromechanical poroelastic finite element and shear-lag models of tendon predict large strain dependent Poisson's ratios and fluid expulsion under tensile loading.Acta Biomater. 2015 Aug;22:83-91. doi: 10.1016/j.actbio.2015.04.035. Epub 2015 Apr 29. Acta Biomater. 2015. PMID: 25934322 Free PMC article.
-
Simulation of high tensile Poisson's ratios of articular cartilage with a finite element fibril-reinforced hyperelastic model.Med Eng Phys. 2008 Jun;30(5):590-8. doi: 10.1016/j.medengphy.2007.06.004. Epub 2007 Aug 8. Med Eng Phys. 2008. PMID: 17690001
-
Poisson's Ratio of Glasses, Ceramics, and Crystals.Materials (Basel). 2024 Jan 7;17(2):300. doi: 10.3390/ma17020300. Materials (Basel). 2024. PMID: 38255468 Free PMC article. Review.
Cited by
-
Three-Dimensional Quantification of Collagen Microstructure During Tensile Mechanical Loading of Skin.Front Bioeng Biotechnol. 2021 Mar 3;9:642866. doi: 10.3389/fbioe.2021.642866. eCollection 2021. Front Bioeng Biotechnol. 2021. PMID: 33748088 Free PMC article.
-
Elastin governs the mechanical response of medial collateral ligament under shear and transverse tensile loading.Acta Biomater. 2015 Oct;25:304-12. doi: 10.1016/j.actbio.2015.07.011. Epub 2015 Jul 7. Acta Biomater. 2015. PMID: 26162584 Free PMC article.
-
Osmotic pressure induced tensile forces in tendon collagen.Nat Commun. 2015 Jan 22;6:5942. doi: 10.1038/ncomms6942. Nat Commun. 2015. PMID: 25608644 Free PMC article.
-
A quantitative study of the relationship between the distribution of different types of collagen and the mechanical behavior of rabbit medial collateral ligaments.PLoS One. 2014 Jul 25;9(7):e103363. doi: 10.1371/journal.pone.0103363. eCollection 2014. PLoS One. 2014. PMID: 25062068 Free PMC article.
-
Helical nanofiber yarn enabling highly stretchable engineered microtissue.Proc Natl Acad Sci U S A. 2019 May 7;116(19):9245-9250. doi: 10.1073/pnas.1821617116. Epub 2019 Apr 24. Proc Natl Acad Sci U S A. 2019. PMID: 31019088 Free PMC article.
References
-
- Adeeb S, Ali A, et al. Modelling the behaviour of ligaments: a technical note. Comput Methods Biomech Biomed Engin. 2004;7(1):33–42. - PubMed
-
- Atkinson TS, Haut RC, et al. A poroelastic model that predicts some phenomenological responses of ligaments and tendons. J Biomech Eng. 1997;119(4):400–5. - PubMed
-
- Ault HK, Hoffman AH. A composite micromechanical model for connective tissues: Part II--Application to rat tail tendon and joint capsule. J Biomech Eng. 1992;114(1):142–6. - PubMed
-
- Baek GH, Carlin GJ, et al. Quantitative analysis of collagen fibrils of human cruciate and meniscofemoral ligaments. Clin Orthop Relat Res. 1998;(357):205–11. - PubMed
-
- Beatty MF, Stalnaker DO. The Poisson function of finite elasticity. Journal of applied mechanics. 1986;53(4):807–813.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

