A population genetic hidden Markov model for detecting genomic regions under selection

Abstract

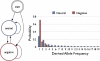
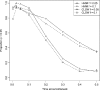
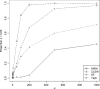
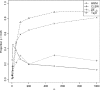
Recently, hidden Markov models have been applied to numerous problems in genomics. Here, we introduce an explicit population genetics hidden Markov model (popGenHMM) that uses single nucleotide polymorphism (SNP) frequency data to identify genomic regions that have experienced recent selection. Our popGenHMM assumes that SNP frequencies are emitted independently following diffusion approximation expectations but that neighboring SNP frequencies are partially correlated by selective state. We give results from the training and application of our popGenHMM to a set of early release data from the Drosophila Population Genomics Project (dpgp.org) that consists of approximately 7.8 Mb of resequencing from 32 North American Drosophila melanogaster lines. These results demonstrate the potential utility of our model, making predictions based on the site frequency spectrum (SFS) for regions of the genome that represent selected elements.

FIG. 1.

A two-state popGenHMM. To the left, a graphical representation of the popGenHMM is shown with states depicted by nodes and transitions among states shown with the unlabeled edges. As the model is Markovian, the sum of all transition probabilities exiting a node sum to 1. To the right, a histogram representing the expected SFS from each of the states of the model is given, assuming a sample size of n = 20. Two states are shown, a neutral state (blue) that emits allele frequencies based on the neutral SFS shown to the right and a state labeled negative (red) that represents a selected state. In this case, selection is negative (α = – 10) and the corresponding SFS for emissions is shown to the right. Note that for a two-state popGenHMM, the selected state need not be negative.

FIG. 2.

A three-state popGenHMM. To the left, a graphical representation of the popGenHMM is shown with states depicted by nodes and transitions among states shown with the unlabeled edges. See caption of figure 1 for details. To the right, a histogram representing the expected SFS from each of the states of the model is given, assuming a sample size of n = 20. Three states are shown, a neutral state (blue), a selected state labeled negative (red) (α = – 10), and a second selected state labeled positive (yellow) (α = 10).

FIG. 3.

Proportion of bottleneck simulations rejecting neutrality. Shown is a comparison of the false-positive rate of the popGenHMM and the CLRT of Kim and Stephan (2002). Two severities of the strength of the bottleneck are shown f = 0.05 and f = 0.1 for each model.

FIG. 4.

Power to detect a single selective sweep. Shown is a comparison of the power of our popGenHMM as a function of the strength of selection, α = 2Ns, in comparison with CLSW (Kim and Stephan 2002), SweepFinder (Nielsen et al. 2005), and a sliding window implementation of Tajima's D (Tajima 1989). Each point consists of 1,000 coalescent simulations with a single selective sweep (stochastic trajectory) that has finished its sojourn through the population just before the current generation (τ = 0). We simulated 20 kb from samples of size n = 50 with θ/bp = 0.01 and ρ/bp = 0.025.

FIG. 5.

Power to detect a locus undergoing recurrent directional selection. Shown is a comparison of the power of our popGenHMM as a function of the strength of selection, α = 2Nσ, in comparison with CLSW (Kim and Stephan 2002), SweepFinder (Nielsen et al. 2005), and a sliding window implementation of Tajima's D (Tajima 1989) to detect selection on a locus evolving according to the normal shift model. Each point consists of 1,000 samples drawn from forward population genetic simulations in which we simulated 20 kb from samples of size n = 50 with θ/bp = 0.01 and ρ/bp = 0.025. Selected sites occur in the middle fifth of the simulated locus (bases 8,000–12,000) and θ is constant across the entire region.

FIG. 6.

Power to detect a locus undergoing recurrent negative selection. Shown is a comparison of the power of our popGenHMM as a function of the strength of selection, α = 2Nσ, SweepFinder (Nielsen et al. 2005) and a sliding window implementation of Tajima's D (Tajima 1989) to detect selection on a locus evolving according to the exponential shift model. Each point consists of 1,000 samples drawn from forward population genetic simulations in which we simulated 20 kb from samples of size n = 50 with θ/bp = 0.01 and ρ/bp = 0.025. Selected sites occur in the middle fifth of the simulated locus (bases 8,000–12,000) and θ is constant across the entire region.

FIG. 7.

Distribution of length normalized scores for elements. Shown are histograms of LOD scores/length (s) for each of the elements predicted. Negatively selected elements are shown in the top panel and positively selected elements in the bottom panel. The very different distributions is a function of the short lengths of positive elements predicted.

FIG. 8.

Browser shot of a negatively selected element prediction. This negative element prediction is shown as the top browser track for this region of the genome. This element has a strong prediction corresponding to a LOD score of 33.1. Shown below the prediction are two tracks corresponding to divergence between Drosophila simulans and D. melanogaster (labeled Div) and nucleotide diversity (π; Tajima 1983) within D. melanogaster (labeled Pi). For both these tracks, darker colors represent greater relative levels of divergence and polymorphism. See text for details.

FIG. 9.

Browser shot of a positively selected element prediction. This positive element prediction is shown as the fourth browser track from the top for this region of the genome. This element has a prediction score of LOD = 29.6. See caption of figure 5 for details.