Optimal in silico target gene deletion through nonlinear programming for genetic engineering
- PMID: 20195367
- PMCID: PMC2827548
- DOI: 10.1371/journal.pone.0009331
Optimal in silico target gene deletion through nonlinear programming for genetic engineering
Abstract
Background: Optimal selection of multiple regulatory genes, known as targets, for deletion to enhance or suppress the activities of downstream genes or metabolites is an important problem in genetic engineering. Such problems become more feasible to address in silico due to the availability of more realistic dynamical system models of gene regulatory and metabolic networks. The goal of the computational problem is to search for a subset of genes to knock out so that the activity of a downstream gene or a metabolite is optimized.
Methodology/principal findings: Based on discrete dynamical system modeling of gene regulatory networks, an integer programming problem is formulated for the optimal in silico target gene deletion problem. In the first result, the integer programming problem is proved to be NP-hard and equivalent to a nonlinear programming problem. In the second result, a heuristic algorithm, called GKONP, is designed to approximate the optimal solution, involving an approach to prune insignificant terms in the objective function, and the parallel differential evolution algorithm. In the third result, the effectiveness of the GKONP algorithm is demonstrated by applying it to a discrete dynamical system model of the yeast pheromone pathways. The empirical accuracy and time efficiency are assessed in comparison to an optimal, but exhaustive search strategy.
Significance: Although the in silico target gene deletion problem has enormous potential applications in genetic engineering, one must overcome the computational challenge due to its NP-hardness. The presented solution, which has been demonstrated to approximate the optimal solution in a practical amount of time, is among the few that address the computational challenge. In the experiment on the yeast pheromone pathways, the identified best subset of genes for deletion showed advantage over genes that were selected empirically. Once validated in vivo, the optimal target genes are expected to achieve higher genetic engineering effectiveness than a trial-and-error procedure.
Conflict of interest statement
Figures




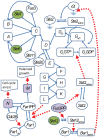
 , Ste5, Ste11, Ste7 and the dephosphorylation of Fu3PP are not shown in the diagram since they are less dominant than those shown in the pheromone pathway.
, Ste5, Ste11, Ste7 and the dephosphorylation of Fu3PP are not shown in the diagram since they are less dominant than those shown in the pheromone pathway.


Similar articles
-
Evolutionary programming as a platform for in silico metabolic engineering.BMC Bioinformatics. 2005 Dec 23;6:308. doi: 10.1186/1471-2105-6-308. BMC Bioinformatics. 2005. PMID: 16375763 Free PMC article.
-
Reverse engineering genetic networks using nonlinear saturation kinetics.Biosystems. 2019 Aug;182:30-41. doi: 10.1016/j.biosystems.2019.103977. Epub 2019 Jun 8. Biosystems. 2019. PMID: 31185246
-
Identifying quantitative operation principles in metabolic pathways: a systematic method for searching feasible enzyme activity patterns leading to cellular adaptive responses.BMC Bioinformatics. 2009 Nov 24;10:386. doi: 10.1186/1471-2105-10-386. BMC Bioinformatics. 2009. PMID: 19930714 Free PMC article.
-
Chemical-genetic approaches for exploring the mode of action of natural products.Prog Drug Res. 2008;66:237, 239-71. doi: 10.1007/978-3-7643-8595-8_5. Prog Drug Res. 2008. PMID: 18416308 Review.
-
Transcriptional networks: reverse-engineering gene regulation on a global scale.Curr Opin Microbiol. 2004 Dec;7(6):638-46. doi: 10.1016/j.mib.2004.10.009. Curr Opin Microbiol. 2004. PMID: 15556037 Review.
References
-
- Sticklen MB. Plant genetic engineering for biofuel production: towards affordable cellulosic ethanol. Nature Reviews Genetics. 2008;9:433–443. - PubMed
-
- Deutscher D, Meilijson I, Kupiec M, Ruppin E. Multiple knockout analysis of genetic robustness in the yeast metabolic network. Nature Genetics. 2006;38:993–998. - PubMed
-
- Nakae J, Oki M, Cao Y. The FoxO transcription factors and metabolic regulation. FEBS Letters. 2008;582:54–67. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases
Miscellaneous

