Correcting the actual reproduction number: a simple method to estimate R(0) from early epidemic growth data
- PMID: 20195446
- PMCID: PMC2819789
- DOI: 10.3390/ijerph7010291
Correcting the actual reproduction number: a simple method to estimate R(0) from early epidemic growth data
Abstract
The basic reproduction number, R(0), a summary measure of the transmission potential of an infectious disease, is estimated from early epidemic growth rate, but a likelihood-based method for the estimation has yet to be developed. The present study corrects the concept of the actual reproduction number, offering a simple framework for estimating R(0) without assuming exponential growth of cases. The proposed method is applied to the HIV epidemic in European countries, yielding R(0) values ranging from 3.60 to 3.74, consistent with those based on the Euler-Lotka equation. The method also permits calculating the expected value of R(0) using a spreadsheet.
Keywords: AIDS; HIV; basic reproduction number; epidemiology; estimation techniques; infectious diseases; statistical model; transmission.
Figures
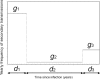


Similar articles
-
Pros and cons of estimating the reproduction number from early epidemic growth rate of influenza A (H1N1) 2009.Theor Biol Med Model. 2010 Jan 7;7:1. doi: 10.1186/1742-4682-7-1. Theor Biol Med Model. 2010. PMID: 20056004 Free PMC article.
-
Comparative estimation of the reproduction number for pandemic influenza from daily case notification data.J R Soc Interface. 2007 Feb 22;4(12):155-66. doi: 10.1098/rsif.2006.0161. J R Soc Interface. 2007. PMID: 17254982 Free PMC article.
-
Definition and estimation of an actual reproduction number describing past infectious disease transmission: application to HIV epidemics among homosexual men in Denmark, Norway and Sweden.Epidemiol Infect. 2004 Dec;132(6):1139-49. doi: 10.1017/s0950268804002997. Epidemiol Infect. 2004. PMID: 15635973 Free PMC article.
-
Estimating epidemic exponential growth rate and basic reproduction number.Infect Dis Model. 2020 Jan 8;5:129-141. doi: 10.1016/j.idm.2019.12.009. eCollection 2020. Infect Dis Model. 2020. PMID: 31956741 Free PMC article. Review.
-
[HIV and AIDS epidemic in Poland and Europe].Przegl Lek. 2003;60 Suppl 6:95-8. Przegl Lek. 2003. PMID: 15106468 Review. Polish.
Cited by
-
Spatiotemporal multi-disease transmission dynamic measure for emerging diseases: an application to dengue and zika integrated surveillance in Thailand.BMC Med Res Methodol. 2019 Oct 26;19(1):200. doi: 10.1186/s12874-019-0833-6. BMC Med Res Methodol. 2019. PMID: 31655546 Free PMC article.
-
Frequent implementation of interventions may increase HIV infections among MSM in China.Sci Rep. 2018 Jan 11;8(1):451. doi: 10.1038/s41598-017-18743-7. Sci Rep. 2018. PMID: 29323225 Free PMC article.
-
The impact of model building on the transmission dynamics under vaccination: observable (symptom-based) versus unobservable (contagiousness-dependent) approaches.PLoS One. 2013 Apr 12;8(4):e62062. doi: 10.1371/journal.pone.0062062. Print 2013. PLoS One. 2013. PMID: 23593507 Free PMC article.
-
A multi-method approach to modeling COVID-19 disease dynamics in the United States.Sci Rep. 2021 Jun 14;11(1):12426. doi: 10.1038/s41598-021-92000-w. Sci Rep. 2021. PMID: 34127757 Free PMC article.
-
Estimation of basic reproduction number for COVID-19 and the reasons for its differences.Int J Clin Pract. 2020 Aug;74(8):e13518. doi: 10.1111/ijcp.13518. Int J Clin Pract. 2020. PMID: 32301199 Free PMC article. No abstract available.
References
-
- Diekmann O, Heesterbeek JA, Metz JA. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–381. - PubMed
-
- Dietz K. The estimation of the basic reproduction number for infectious diseases. Stat. Methods. Med. Res. 1993;2:23–41. - PubMed
-
- Becker NG. Analysis of Infectious Disease Data. Chapman & Hall; Boca Raton, FL, USA: 1989.
-
- Smith CE. Factors in the transmission of virus infections from animal to man. Sci Basis Med Ann Rev. 1964:125–150. - PubMed
-
- Kendall DG. Proceedings of the 3rd Berkeley Symposium on Mathematical Statistics and Probability. University of California Press; Berkeley, CA, USA: 1956. Deterministic and stochastic epidemics in closed populations; pp. 149–165.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

