Review: Semiconductor Piezoresistance for Microsystems

Abstract

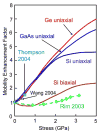
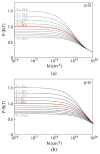
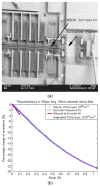
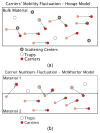
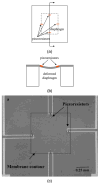
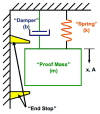
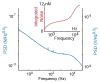
Piezoresistive sensors are among the earliest micromachined silicon devices. The need for smaller, less expensive, higher performance sensors helped drive early micromachining technology, a precursor to microsystems or microelectromechanical systems (MEMS). The effect of stress on doped silicon and germanium has been known since the work of Smith at Bell Laboratories in 1954. Since then, researchers have extensively reported on microscale, piezoresistive strain gauges, pressure sensors, accelerometers, and cantilever force/displacement sensors, including many commercially successful devices. In this paper, we review the history of piezoresistance, its physics and related fabrication techniques. We also discuss electrical noise in piezoresistors, device examples and design considerations, and alternative materials. This paper provides a comprehensive overview of integrated piezoresistor technology with an introduction to the physics of piezoresistivity, process and material selection and design guidance useful to researchers and device engineers.

Fig. 1

The alteration of specific resistance produced in different metals by hammering-induced strain. After Tomlinson, 1883 [5]. Reprinted with permission from the Royal Society Publishing.

Fig. 2

Modern micromachined, precision-etched silicon gages with welded lead wires. (a) Bar shaped strain gauge with a length of 6 mm. (b) U-shaped strain gauge with a length of 1.2 mm. Courtesy of Herb Chelner, Micron Instruments, Simi Valley, CA.

Fig. 3

Technological advances in IC fabrication (above the horizontal line) and micromachining (below the horizontal line) [30], [33]–[37], [47], [79], [112], [122], [130], [149], [160], [191], [251], [254], [268], [284], [372]–[384].

Fig. 4

(a) Covalently bonded diamond cubic structure of silicon. (b) Commonly employed crystal planes of silicon, i.e., (100), (110), and (111) planes. Silicon has four covalent bonds and coordinates itself tetrahedrally. The {111} planes, oriented 54.74° from {100} planes, are most densely packed. Mechanical and electrical properties vary greatly with direction, especially between the most dense {111} and the least dense {100} planes.

Fig. 5

Nine components, σ_ij, of stress on an infinitesimal unit element. For clarity, stresses on negative faces are not depicted.

Fig. 6

Notation for Smith’s test configurations. Configurations A and C measured longitudinal piezoresistance, while configurations B and D provided transverse coefficients. Voltage drops between the electrodes (dotted lines) were measured while uniaxial tensile stress, σ, was applied to the test sample by hanging a weight. The experiments were done in constant-current mode in a light-tight enclosure with controlled temperature (25 ± 1 °C). After Smith [30]. © 1954 American Physical Society, http://www.prola.aps.org/abstract/PR/v94/i1/p42_1.

Fig. 7

Energy bands split in diamond and are a function of strain or atomic spacing, R (Atomic Units). Besides the four shaded bands, there are four bands of zero width, i.e. two following curve IV and two following curve VI. After Kimball [74]. © 1935 American Institute of Physics.

Fig. 8

(a, b) Test configuration and resulting schematic diagrams of probable constant energy surfaces in momentum space for n-type Si with potential, E, and strain, e, as depicted. The electrons are located in six energy valleys at the centers of the constant energy ellipses, which are shown greatly enlarged. The effect of stress on the two valley energies shown is indicated by the dotted ellipsoids. The mobilities, μ, of the several groups of charge carriers in various directions are roughly indicated by the arrows. The test configurations correspond to Smith’s experimental arrangements A and C (Fig. 6). After Smith [30]. © 1954 American Physical Society. (c) The changes in silicon energy minima with dilation in a plane normal to a (001) axis. Four minima vary as shown by the solid line, and two on the axis normal to the plane follow the dashed line. After Keyes [87], © 2002 IEEE.

Fig. 9

Hole mobility enhancement in semiconductors, taking into account surface roughness scattering, as a function of stress (~GPa). Sun et al. compared their experimental results with those of several groups [385]–[387] and noted that “the hole mobilities of Ge and GaAs increase steadily with stress up to 4 GPa, while the hole mobility of Si saturates at about 2 GPa. For the technologically important stresses of 1–2 GPa, Ge shows similar enhancement as Si. However the unstressed hole mobility of Ge is ~3× higher than Si.” Reprinted with permission from Sun [73], © 2007 American Institute of Physics.

Fig. 10

(a) Microfabricated piezoresistive cantilever [57]. (b) TSUPREM4 [388] simulation plots of doping profiles using ion implantation vs. epitaxial deposition techniques. Note the difference in the dopant profiles following ion-implantation and epitaxy and the progression of dopant diffusion with increasing time of thermal annealing. Courtesy of Sung-Jin Park, Stanford University.

Fig. 11

Room temperature piezoresistive coefficients in the (100) plane of (a) p-type silicon (b) n-type silicon. These graphics predict piezoresistive coefficients very well for low doses. After Kanda [47], © 1982 IEEE.

Fig. 12

Piezoresistive coefficients as a function of doping. Experimental data obtained by Kerr, Tufte, and Mason are fitted by Harley and Kenny [79], [148], [149], [157]. Theoretical prediction by Kanda overestimates the piezoresistive coefficients at higher concentrations. After Harley and Kenny [149], © 2000 IEEE.

Fig. 13

The adjusted piezoresistance factor P(N,T) as a function of impurity concentration and temperature for (a) p-type silicon (b) n-type silicon. These graphics predict piezoresistive coefficients very well for low doses but the trends with temperature are correct. After Kanda [47], © 1982 IEEE.

Fig. 14

(a) Stress sensor chip with a p-type circular piezoresistors in the middle of the chip. (b) Schematic diagram of the circular piezoresistor with a radius of 1700 μm. From Richter et al. [154], © 2007 IEEE.

Fig. 15

Trends of key piezoresistive properties with concentrations, such as (a) longitudinal piezoresistive coefficient (sensitivity) (b) temperature coefficient of sensitivity (c) temperature coefficient of resistivity with dopant concentration. After Kurtz and Gravel [147]. © 1967 Industrial Automation Standards.

Fig. 16

(a) SEM image of micro-actuator and 150-μm-long, 150-nm-diameter, phosphorous-doped, 〈110〉 silicon fiber (test sample) with resistivity of 0.6 mΩcm. (b) Percentage change longitudinal piezoresistance vs. strain exhibited less nonlinearity at low strain than previous reports at lower doping (Data of Matsuda et al. [161] were included by converting stress data using Young’s modulus of 170 GPa). Reprinted with permission from Chen and MacDonald [161], © 2004 American Institute of Physics.

Fig. 17

Conductivity fluctuations based on (a) Hooge model (bulk effect) (b) McWhorter model (surface effect). Courtesy of Paul Lim, Stanford University.

Fig. 18

Hooge noise parameter, α, improves (decreases) with increasing anneal diffusion length, √Dt. Reprinted with permission from Mallon et al. [56]. © 2008 American Institute of Physics.

Fig. 19

Typical noise curve of a full-bridged piezoresistor. The sloped solid line is the total noise dominated by 1/f-noise component, while the horizontal solid line is the total noise dominated by thermal-noise component. The 1/f noise corner frequency is the frequency at which the thermal noise is equal to the 1/f noise. In this noise spectrum, the corner frequency is ~1 Hz. The horizontal dashed line is the measurement system noise level, which is verified with a 680 Ω resistor from 0.01 Hz. For clarity, system noise is not shown above 1 Hz. The noise is measured using modulation-demodulation technique (Section III-E). The roll-off above 60 Hz is due to system bandwidth. Reprinted with permission from Mallon et al. [56]. © 2008 American Institute of Physics.

Fig. 20

A cantilever with applied force at the tip and the resulting stress profile in the beam. The maximum stress occurs at outer surface of the root (y = ±h/2, x = 0).

Fig. 21

(a) Dual-axis AFM cantilever with orthogonal axes of compliance. Oblique ion implants are used to form electrical elements on vertical sidewalls and horizontal surfaces simultaneously. (b) SEM Image of a dual-axis AFM cantilever. Reprinted with permission from Chui et al. [122]. © 1998 American Institute of Physics.

Fig. 22

Illustration of a piezoresistive pressure sensor. (a) Top view of piezoresistive pressure sensor. Four piezoresistors are placed on each edge forming a Wheatstone bridge circuit. (b) Cross section A-A showing deflected diaphragm with piezoresistors at maximum stress locations. (c) Photograph of a pressure sensors with four 3C-SiC (a polytype of silicon carbide, see Section IV-A) piezoresistors. From Wu et al. [336]. © 2000 IEEE.

Fig. 23

The evolution of micromachined pressure sensors from 1950s to 1980s. After Eaton and Smith [102].

Fig. 24

Bosch porous silicon pressure sensor. (a) Sensing diaphragm and cavity cross section. (b) Pressure sensor with mixed signal integrated CMOS signal conditioning electronics. (c) Ceramic surface mount packaged sensor. © Bosch. Pictures: Bosch.

Fig. 25

An accelerometer is modeled as a second order system with a proof mass (m), spring (k), and damper (b). The displacement (x) is proportional to the acceleration (A) in the x-direction. The range of the proof mass movement is limited by the end stops, which protect the device from shock damage.

Fig. 26

(a) Oblique-view SEM of a sidewall-implanted (41° from the vertical axis) piezoresistive accelerometer with a 20-μm-thick epi-poly encapsulation. (b) Optical photograph of the completely packaged piezoresistive accelerometer with flexible circuit wiring. The sensor is shown in the background of table salt crystals. From Park et al. [276]. © 2007 IEEE.

Fig. 27

A MEMS gyroscope is driven in one axis and sensed in an orthogonal axis.

Fig. 28

Gyroscope with electromagnetic excitation and piezoresistive detection. From Paoletti [278]. © 1996 IEEE.

Fig. 29

(a) Piezoresistive floating-element MEMS shear stress sensor. Each sensor consists of two top-implanted and two sidewall-implanted piezoresistors. The sidewall-implanted piezoresistors are sensitive to in-plane stress (shear stress), while the top-implanted piezoresistors are sensitive to out-of-plane stress (normal stress). Thus, each sensor enables simultaneous measurements of normal and shear stresses. (b) SEM image of a 500-μm square floating element. (c) SEM image of one of the tethers with a sidewall-implanted piezoresistor. Reprinted from Barlian et al. [53] with permission from Elsevier.

Fig. 30

(a) CMOS integrated piezoresistive cantilever array (two scanning cantilevers and one reference cantilever) (b) Micrograph of the overall sensor CMOS signal conditioning circuit (c) Array of 12 cantilevers (the inner ten can be used for scanning while the outer two serve as a reference). The dimensions of the scanning cantilevers are 500 μm × 85 μm. From Hafizovic et al. [305], reprinted with permission from PNAS.

Fig. 31

The power spectral density (PSD) and integrated force noise of a measurement system using an AD622 instrumentation amplifier and piezoresistor bridge. All components in a signal conditioning circuit contribute to the noise and resolution of the system. Courtesy of Sung-Jin Park [54], reprinted with permission from PNAS.

Fig. 32

Modulation-demodulation circuit for low frequency low noise detection.

Fig. 33

Longitudinal gauge factor in 〈100〉 direction for β-SiC as a function of temperature for different doping levels from various researchers [324], [325]. Werner et al. noted that these experimental data are in good agreement with the theoretical gauge factor predicted by electron transfer mechanism theory [81] in many-valley semiconductors [328]. After Werner et al. [328]. Reprinted with permission from Wiley.

Fig. 34

The summary of published average longitudinal and transverse piezoresistance coefficients in boron-doped polycrystalline diamond by Werner et al. [342]. The published gauge factor data were converted to piezoresistive coefficients assuming Young’s modulus of 1143 × 10⁹ Pa. After Werner et al. [342]. © 1998 IEEE.

Fig. 35

(a) Schematic of a CNT device on a membrane (b) Optical microscope image of a membrane with electrodes (c) Zoomed in image of devices near the edge of a membrane (d) SEM Image of a CNT crossing the gap between two electrodes (~800 nm). Reprinted with permission from Grow [353]. © 2005 American Institute of Physics.

Fig. 36

Size (cross sectional area) effect on longitudinal and transverse piezoresistive coefficients in boron-doped nanowires fabricated using electron beam (EB) lithography and reactive-ion-etching (RIE). After Toriyama [366]. © 2002 IEEE.

Fig. 37

(a) A 〈111〉 nanowire grown and anchored onto a silicon substrate. (b) morphology of a bridged nanowire along the 〈111〉 direction. (c) Transmission Electron Microscopy (TEM) images of the left joint between the sidewall and the nanowire bridge. (d) Longitudinal piezoresistive coefficients of 〈111〉 nanowires as a function of the nanowire diameter and resistivity. Piezoresistive coefficients from bulk silicon are also included. The scale bars in (a)–(c) are 2 μm, 500 nm, and 100 nm, respectively. From He and Yang [369]. Reprinted with permission from Macmillan Publishers Ltd.: Nature Nanotechnology [369] © 2006.