Estimation of inferential uncertainty in assessing expert segmentation performance from STAPLE
- PMID: 20199913
- PMCID: PMC3183509
- DOI: 10.1109/TMI.2009.2036011
Estimation of inferential uncertainty in assessing expert segmentation performance from STAPLE
Abstract
The evaluation of the quality of segmentations of an image, and the assessment of intra- and inter-expert variability in segmentation performance, has long been recognized as a difficult task. For a segmentation validation task, it may be effective to compare the results of an automatic segmentation algorithm to multiple expert segmentations. Recently an expectation-maximization (EM) algorithm for simultaneous truth and performance level estimation (STAPLE) was developed to this end to compute both an estimate of the reference standard segmentation and performance parameters from a set of segmentations of an image. The performance is characterized by the rate of detection of each segmentation label by each expert in comparison to the estimated reference standard. This previous work provides estimates of performance parameters,but does not provide any information regarding the uncertainty of the estimated values. An estimate of this inferential uncertainty, if available, would allow the estimation of confidence intervals for the values of the parameters. This would facilitate the interpretation of the performance of segmentation generators and help determine if sufficient data size and number of segmentations have been obtained to precisely characterize the performance parameters. We present a new algorithm to estimate the inferential uncertainty of the performance parameters for binary and multi-category segmentations. It is derived for the special case of the STAPLE algorithm based on established theory for general purpose covariance matrix estimation for EM algorithms. The bounds on the performance parameters are estimated by the computation of the observed information matrix.We use this algorithm to study the bounds on performance parameters estimates from simulated images with specified performance parameters, and from interactive segmentations of neonatal brain MRIs. We demonstrate that confidence intervals for expert segmentation performance parameters can be estimated with our algorithm. We investigate the influence of the number of experts and of the segmented data size on these bounds, showing that it is possible to determine the number of image segmentations and the size of images necessary to achieve a chosen level of accuracy in segmentation performance assessment.
Figures


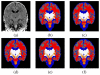
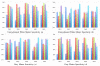
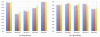

Similar articles
-
Estimation of inferential uncertainty in assessing expert segmentation performance from STAPLE.Inf Process Med Imaging. 2009;21:701-12. doi: 10.1007/978-3-642-02498-6_58. Inf Process Med Imaging. 2009. PMID: 19694305 Free PMC article.
-
Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation.IEEE Trans Med Imaging. 2004 Jul;23(7):903-21. doi: 10.1109/TMI.2004.828354. IEEE Trans Med Imaging. 2004. PMID: 15250643 Free PMC article.
-
Incorporating priors on expert performance parameters for segmentation validation and label fusion: a maximum a posteriori STAPLE.Med Image Comput Comput Assist Interv. 2010;13(Pt 3):25-32. doi: 10.1007/978-3-642-15711-0_4. Med Image Comput Comput Assist Interv. 2010. PMID: 20879379 Free PMC article.
-
Estimating a reference standard segmentation with spatially varying performance parameters: local MAP STAPLE.IEEE Trans Med Imaging. 2012 Aug;31(8):1593-606. doi: 10.1109/TMI.2012.2197406. Epub 2012 May 2. IEEE Trans Med Imaging. 2012. PMID: 22562727 Free PMC article.
-
Machines that learn to segment images: a crucial technology for connectomics.Curr Opin Neurobiol. 2010 Oct;20(5):653-66. doi: 10.1016/j.conb.2010.07.004. Curr Opin Neurobiol. 2010. PMID: 20801638 Free PMC article. Review.
Cited by
-
The effect of imaging modality (magnetic resonance imaging vs. computed tomography) and patient position (supine vs. prone) on target and organ at risk doses in partial breast irradiation.J Med Radiat Sci. 2021 Jun;68(2):157-166. doi: 10.1002/jmrs.453. Epub 2020 Dec 7. J Med Radiat Sci. 2021. PMID: 33283982 Free PMC article.
-
Validating retinal fundus image analysis algorithms: issues and a proposal.Invest Ophthalmol Vis Sci. 2013 May 1;54(5):3546-59. doi: 10.1167/iovs.12-10347. Invest Ophthalmol Vis Sci. 2013. PMID: 23794433 Free PMC article.
-
A collaborative resource to build consensus for automated left ventricular segmentation of cardiac MR images.Med Image Anal. 2014 Jan;18(1):50-62. doi: 10.1016/j.media.2013.09.001. Epub 2013 Sep 13. Med Image Anal. 2014. PMID: 24091241 Free PMC article.
-
Comparative performance evaluation of automated segmentation methods of hippocampus from magnetic resonance images of temporal lobe epilepsy patients.Med Phys. 2016 Jan;43(1):538. doi: 10.1118/1.4938411. Med Phys. 2016. PMID: 26745947 Free PMC article.
-
Two-dimensional segmentation fusion tool: an extensible, free-to-use, user-friendly tool for combining different bidimensional segmentations.Front Bioeng Biotechnol. 2024 Jan 31;12:1339723. doi: 10.3389/fbioe.2024.1339723. eCollection 2024. Front Bioeng Biotechnol. 2024. PMID: 38357706 Free PMC article.
References
-
- Huttenlocher D, Klanderman D, Rucklige A. Comparing images using the Hausdorff distance. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1993 Sep;vol. 15(no. 9):850–863.
-
- Chalana V, Kim Y. A methodology for evaluation of boundary detection algorithms on medical images. IEEE Transactions on Medical Imaging. 1997;vol. 16(no. 5):642–652. - PubMed
-
- Dice L. Measures of the amount of ecologic association between species. Ecology. 1945;vol. 26(no. 3):297–302.
-
- Jaccard P. The distribution of flora in the alpine zone. New Phytologist. 1912;vol. 11:37–50.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

