Application and evaluation of a measured spatially variant system model for PET image reconstruction
- PMID: 20199927
- PMCID: PMC2903538
- DOI: 10.1109/TMI.2010.2040188
Application and evaluation of a measured spatially variant system model for PET image reconstruction
Abstract
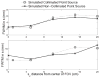
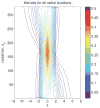
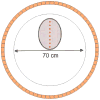
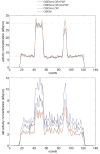
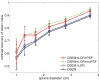
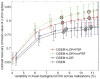
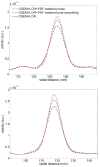
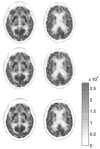
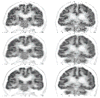
Accurate system modeling in tomographic image reconstruction has been shown to reduce the spatial variance of resolution and improve quantitative accuracy. System modeling can be improved through analytic calculations, Monte Carlo simulations, and physical measurements. The purpose of this work is to improve clinical fully-3-D reconstruction without substantially increasing computation time. We present a practical method for measuring the detector blurring component of a whole-body positron emission tomography (PET) system to form an approximate system model for use with fully-3-D reconstruction. We employ Monte Carlo simulations to show that a non-collimated point source is acceptable for modeling the radial blurring present in a PET tomograph and we justify the use of a Na22 point source for collecting these measurements. We measure the system response on a whole-body scanner, simplify it to a 2-D function, and incorporate a parameterized version of this response into a modified fully-3-D OSEM algorithm. Empirical testing of the signal versus noise benefits reveal roughly a 15% improvement in spatial resolution and 10% improvement in contrast at matched image noise levels. Convergence analysis demonstrates improved resolution and contrast versus noise properties can be achieved with the proposed method with similar computation time as the conventional approach. Comparison of the measured spatially variant and invariant reconstruction revealed similar performance with conventional image metrics. Edge artifacts, which are a common artifact of resolution-modeled reconstruction methods, were less apparent in the spatially variant method than in the invariant method. With the proposed and other resolution-modeled reconstruction methods, edge artifacts need to be studied in more detail to determine the optimal tradeoff of resolution/contrast enhancement and edge fidelity.
Figures








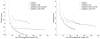





References
-
- Schmitt D, Karuta B, Carrier C, Lecomte R. Fast point spread function computation from aperture functions in high-resolution positron emission tomography. IEEE Trans Med Imag. 1988 Mar;7(1):2–12. - PubMed
-
- Strul D, Slates RB, Dahlbom M, Cherry SR, Marsden PK. An improved analytical detector response function model for multilayer small-diameter PET scanners. Phys Med Biol. 2003;48(8):979–994. - PubMed
-
- Qi J, Leahy RM, Cherry SR, Chatziioannou A, Farquhar TH. High-resolution 3-D Bayesian image reconstruction using the microPET small-animal scanner. Phys Med Biol. 1998;43(4):1001–1013. - PubMed
-
- Mumcuoglu E, Leahy R, Cherry S, Hoffman E. Accurate geometric and physical response modelling for statistical image reconstruction in high resolution PET. Proc IEEE Nucl Sci Symp Med Imag Conf. 1996;3:1569–1573.
-
- Frese T, Rouze NC, Bouman CA, Sauer K, Hutchins GD. Quantitative comparison of FBP, EM, and Bayesian reconstruction algorithms for the IndyPET scanner. IEEE Trans Med Imag. 2003 Feb;22(2):258–76. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

