Immersed finite element method and its applications to biological systems
- PMID: 20200602
- PMCID: PMC2830735
- DOI: 10.1016/j.cma.2005.05.049
Immersed finite element method and its applications to biological systems
Abstract
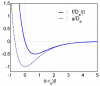
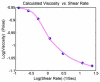
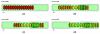
This paper summarizes the newly developed immersed finite element method (IFEM) and its applications to the modeling of biological systems. This work was inspired by the pioneering work of Professor T.J.R. Hughes in solving fluid-structure interaction problems. In IFEM, a Lagrangian solid mesh moves on top of a background Eulerian fluid mesh which spans the entire computational domain. Hence, mesh generation is greatly simplified. Moreover, both fluid and solid domains are modeled with the finite element method and the continuity between the fluid and solid subdomains is enforced via the interpolation of the velocities and the distribution of the forces with the reproducing Kernel particle method (RKPM) delta function. The proposed method is used to study the fluid-structure interaction problems encountered in human cardiovascular systems. Currently, the heart modeling is being constructed and the deployment process of an angioplasty stent has been simulated. Some preliminary results on monocyte and platelet deposition are presented. Blood rheology, in particular, the shear-rate dependent de-aggregation of red blood cell (RBC) clusters and the transport of deformable cells, are modeled. Furthermore, IFEM is combined with electrokinetics to study the mechanisms of nano/bio filament assembly for the understanding of cell motility.
Figures





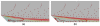







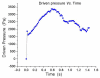
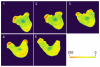
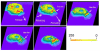
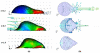

References
-
- Tezduyar TE. Stabilized finite element formulations for incompressible-flow computations. Adv. Appl. Mech. 1992;28:1–44.
-
- Tezduyar TE. Finite element methods for flow problems with moving boundaries and interfaces. Arch. Comput. Methods Engrg. 2001;8(2):83–130.
-
- Huerta A, Liu WK. Viscous flow with large free surface motion. Comput. Methods Appl. Mech. Engrg. 1988;69:277–324.
-
- Hughes TJR, Liu WK, Zimmerman TK. Lagrangian–Eulerian finite element formulations for incompressible viscous flows. Comput. Methods Appl. Mech. Engrg. 1981;29:329–349.
-
- Liu WK. Finite element procedures for fluid–structure interactions and application to liquid storage tanks. Nucl. Engrg. Des. 1981;65:221–238.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
