Predictive coding as a model of response properties in cortical area V1
- PMID: 20203213
- PMCID: PMC6634102
- DOI: 10.1523/JNEUROSCI.4911-09.2010
Predictive coding as a model of response properties in cortical area V1
Abstract
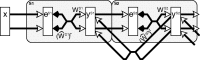
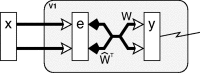
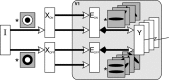
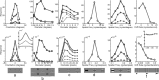
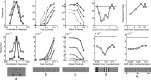
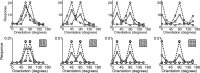
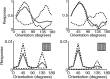
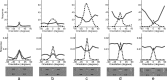
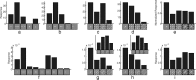
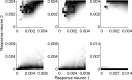
A simple model is shown to account for a large range of V1 classical, and nonclassical, receptive field properties including orientation tuning, spatial and temporal frequency tuning, cross-orientation suppression, surround suppression, and facilitation and inhibition by flankers and textured surrounds. The model is an implementation of the predictive coding theory of cortical function and thus provides a single computational explanation for a diverse range of neurophysiological findings. Furthermore, since predictive coding can be related to the biased competition theory and is a specific example of more general theories of hierarchical perceptual inference, the current results relate V1 response properties to a wider, more unified, framework for understanding cortical function.
Figures


Similar articles
-
A single functional model accounts for the distinct properties of suppression in cortical area V1.Vision Res. 2011 Mar 25;51(6):563-76. doi: 10.1016/j.visres.2011.01.017. Epub 2011 Feb 16. Vision Res. 2011. PMID: 21315102
-
Stimulus-selective spiking is driven by the relative timing of synchronous excitation and disinhibition in cat striate neurons in vivo.Eur J Neurosci. 2008 Oct;28(7):1286-300. doi: 10.1111/j.1460-9568.2008.06434.x. Eur J Neurosci. 2008. PMID: 18973556
-
Emergence of orientation-selective inhibition in the primary visual cortex: a Bayes-Markov computational model.Biol Cybern. 2004 Aug;91(2):115-30. doi: 10.1007/s00422-004-0483-5. Epub 2004 Aug 31. Biol Cybern. 2004. PMID: 15340852
-
Functional cell classes and functional architecture in the early visual system of a highly visual rodent.Prog Brain Res. 2005;149:127-45. doi: 10.1016/S0079-6123(05)49010-X. Prog Brain Res. 2005. PMID: 16226581 Review.
-
Anatomical origins of the classical receptive field and modulatory surround field of single neurons in macaque visual cortical area V1.Prog Brain Res. 2002;136:373-88. doi: 10.1016/s0079-6123(02)36031-x. Prog Brain Res. 2002. PMID: 12143395 Review.
Cited by
-
Adaptation to implied tilt: extensive spatial extrapolation of orientation gradients.Front Psychol. 2013 Jul 19;4:438. doi: 10.3389/fpsyg.2013.00438. eCollection 2013. Front Psychol. 2013. PMID: 23882243 Free PMC article.
-
A neuronal model of predictive coding accounting for the mismatch negativity.J Neurosci. 2012 Mar 14;32(11):3665-78. doi: 10.1523/JNEUROSCI.5003-11.2012. J Neurosci. 2012. PMID: 22423089 Free PMC article.
-
Assessment of water safety competencies: Benefits and caveats of testing in open water.Front Psychol. 2022 Sep 28;13:982480. doi: 10.3389/fpsyg.2022.982480. eCollection 2022. Front Psychol. 2022. PMID: 36248477 Free PMC article. Review.
-
Temporal expectation and attention jointly modulate auditory oscillatory activity in the beta band.PLoS One. 2015 Mar 23;10(3):e0120288. doi: 10.1371/journal.pone.0120288. eCollection 2015. PLoS One. 2015. PMID: 25799572 Free PMC article.
-
Temporal Contingencies Determine Whether Adaptation Strengthens or Weakens Normalization.J Neurosci. 2018 Nov 21;38(47):10129-10142. doi: 10.1523/JNEUROSCI.1131-18.2018. Epub 2018 Oct 5. J Neurosci. 2018. PMID: 30291205 Free PMC article.
References
-
- Adorján P, Levitt JB, Lund JS, Obermayer K. A model for the intracortical origin of orientation preference and tuning in macaque striate cortex. Vis Neurosci. 1999;16:303–318. - PubMed
-
- Albrecht DG, Geisler WS. Motion selectivity and the contrast-response function of simple cells in the visual cortex. Vis Neurosci. 1991;7:531–546. - PubMed
-
- Angelucci A, Bullier J. Reaching beyond the classical receptive field of V1 neurons: horizontal or feedback axons? J Physiol Paris. 2003;97:141–154. - PubMed
-
- Barlow HB. What is the computational goal of the neocortex? In: Koch C, Davis JL, editors. Large-scale neuronal theories of the brain. Cambridge, MA: MIT; 1994. pp. 1–22. Chap 1.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
