Periodic table of virus capsids: implications for natural selection and design
- PMID: 20209096
- PMCID: PMC2831995
- DOI: 10.1371/journal.pone.0009423
Periodic table of virus capsids: implications for natural selection and design
Abstract
Background: For survival, most natural viruses depend upon the existence of spherical capsids: protective shells of various sizes composed of protein subunits. So far, general evolutionary pressures shaping capsid design have remained elusive, even though an understanding of such properties may help in rationally impeding the virus life cycle and designing efficient nano-assemblies.
Principal findings: This report uncovers an unprecedented and species-independent evolutionary pressure on virus capsids, based on the the notion that the simplest capsid designs (or those capsids with the lowest "hexamer complexity", C(h)) are the fittest, which was shown to be true for all available virus capsids. The theories result in a physically meaningful periodic table of virus capsids that uncovers strong and overarching evolutionary pressures, while also offering geometric explanations to other capsid properties (rigidity, pleomorphy, auxiliary requirements, etc.) that were previously considered to be unrelatable properties of the individual virus.
Significance: Apart from describing a universal rule for virus capsid evolution, our work (especially the periodic table) provides a language with which highly diverse virus capsids, unified only by geometry, may be described and related to each other. Finally, the available virus structure databases and other published data reiterate the predicted geometry-derived rules, reinforcing the role of geometry in the natural selection and design of virus capsids.
Conflict of interest statement
Figures
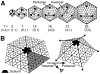
 ).
).
 rule, capsids with high hexamer complexity are under-represented in nature as evident in the observed versus unbiased capsid abundances (
rule, capsids with high hexamer complexity are under-represented in nature as evident in the observed versus unbiased capsid abundances ( of families that display capids of specific
of families that display capids of specific  ). (B)
). (B)  is not conveniently correlated with capsid size (
is not conveniently correlated with capsid size ( ) or class (symbols). (C) However, trends in
) or class (symbols). (C) However, trends in  are easily discerned from the periodic table, where, in each period (row),
are easily discerned from the periodic table, where, in each period (row),  , class number and
, class number and  increase (or remain the same), while trends in other capsid properties such as rigidity may also be deciphered.
increase (or remain the same), while trends in other capsid properties such as rigidity may also be deciphered.
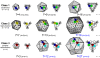
 and
and  ; the diagram arbitrarily assumes that
; the diagram arbitrarily assumes that  ).
).  describes the limit of the geometric domain, beyond which our geometric assumptions and predictions may not hold. We expect that all capsid sizes greater than
describes the limit of the geometric domain, beyond which our geometric assumptions and predictions may not hold. We expect that all capsid sizes greater than  will be exclusively described by continuum elasticity. We also expect that, beyond
will be exclusively described by continuum elasticity. We also expect that, beyond  (i.e., in the purely continuum domain), the Föppl-von Karman number (
(i.e., in the purely continuum domain), the Föppl-von Karman number ( ) , that dictates spherical vs. icosahedral morphology will depend primarily on
) , that dictates spherical vs. icosahedral morphology will depend primarily on  , and so there will be a capsid size (
, and so there will be a capsid size ( ) that demarcates the allowance for spherical and icosahedral morphologies in the purely continuum regime (the sigmoidal curve represents the dependence of
) that demarcates the allowance for spherical and icosahedral morphologies in the purely continuum regime (the sigmoidal curve represents the dependence of  and hence morphology on
and hence morphology on  ). These assumptions consolidate all observed instances of spherical capsid morphology.
). These assumptions consolidate all observed instances of spherical capsid morphology.References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

