THE LAYERED NET SURFACE PROBLEMS IN DISCRETE GEOMETRY AND MEDICAL IMAGE SEGMENTATION
- PMID: 20221409
- PMCID: PMC2834968
- DOI: 10.1142/S0218195907002331
THE LAYERED NET SURFACE PROBLEMS IN DISCRETE GEOMETRY AND MEDICAL IMAGE SEGMENTATION
Abstract
Efficient detection of multiple inter-related surfaces representing the boundaries of objects of interest in d-D images (d >/= 3) is important and remains challenging in many medical image analysis applications. In this paper, we study several layered net surface (LNS) problems captured by an interesting type of geometric graphs called ordered multi-column graphs in the d-D discrete space (d >/= 3 is any constant integer). The LNS problems model the simultaneous detection of multiple mutually related surfaces in three or higher dimensional medical images. Although we prove that the d-D LNS problem (d >/= 3) on a general ordered multi-column graph is NP-hard, the (special) ordered multi-column graphs that model medical image segmentation have the self-closure structures and thus admit polynomial time exact algorithms for solving the LNS problems. Our techniques also solve the related net surface volume (NSV) problems of computing well-shaped geometric regions of an optimal total volume in a d-D weighted voxel grid. The NSV problems find applications in medical image segmentation and data mining. Our techniques yield the first polynomial time exact algorithms for several high dimensional medical image segmentation problems. Experiments and comparisons based on real medical data showed that our LNS algorithms and software are computationally efficient and produce highly accurate and consistent segmentation results.
Figures
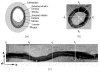
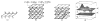

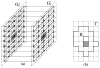
 and
and  . (f) The net model B for ℐ.
. (f) The net model B for ℐ.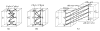
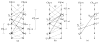
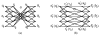
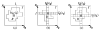
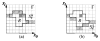
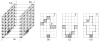
 in G′. (b) The extended “upper” surface
defined by the vertices of
in
in G′. (b) The extended “upper” surface
defined by the vertices of
in  . (c) The extended “lower” surface
defined by the vertices of
in
. (c) The extended “lower” surface
defined by the vertices of
in  . (d) A weakly watershed-monotone region R corresponding to the closed set
. (d) A weakly watershed-monotone region R corresponding to the closed set  .
.



Similar articles
-
EFFICIENT ALGORITHMS FOR THE OPTIMAL-RATIO REGION DETECTION PROBLEMS IN DISCRETE GEOMETRY WITH APPLICATIONS.Int J Comput Geom Appl. 2006;4288:289-299. doi: 10.1007/11940128_30. Int J Comput Geom Appl. 2006. PMID: 25414538 Free PMC article.
-
Optimal surface segmentation in volumetric images--a graph-theoretic approach.IEEE Trans Pattern Anal Mach Intell. 2006 Jan;28(1):119-34. doi: 10.1109/TPAMI.2006.19. IEEE Trans Pattern Anal Mach Intell. 2006. PMID: 16402624 Free PMC article.
-
Optimal graph search segmentation using arc-weighted graph for simultaneous surface detection of bladder and prostate.Med Image Comput Comput Assist Interv. 2009;12(Pt 2):827-35. doi: 10.1007/978-3-642-04271-3_100. Med Image Comput Comput Assist Interv. 2009. PMID: 20426188
-
LOGISMOS--layered optimal graph image segmentation of multiple objects and surfaces: cartilage segmentation in the knee joint.IEEE Trans Med Imaging. 2010 Dec;29(12):2023-37. doi: 10.1109/TMI.2010.2058861. Epub 2010 Jul 19. IEEE Trans Med Imaging. 2010. PMID: 20643602 Free PMC article.
-
A Survey of Graph Cuts/Graph Search Based Medical Image Segmentation.IEEE Rev Biomed Eng. 2018;11:112-124. doi: 10.1109/RBME.2018.2798701. Epub 2018 Jan 26. IEEE Rev Biomed Eng. 2018. PMID: 29994356 Review.
Cited by
-
Multi-surface and multi-field co-segmentation of 3-D retinal optical coherence tomography.IEEE Trans Med Imaging. 2014 Dec;33(12):2242-53. doi: 10.1109/TMI.2014.2336246. Epub 2014 Jul 9. IEEE Trans Med Imaging. 2014. PMID: 25020067 Free PMC article.
-
Automated 3-D intraretinal layer segmentation of macular spectral-domain optical coherence tomography images.IEEE Trans Med Imaging. 2009 Sep;28(9):1436-47. doi: 10.1109/TMI.2009.2016958. Epub 2009 Mar 10. IEEE Trans Med Imaging. 2009. PMID: 19278927 Free PMC article.
-
EFFICIENT ALGORITHMS FOR THE OPTIMAL-RATIO REGION DETECTION PROBLEMS IN DISCRETE GEOMETRY WITH APPLICATIONS.Int J Comput Geom Appl. 2006;4288:289-299. doi: 10.1007/11940128_30. Int J Comput Geom Appl. 2006. PMID: 25414538 Free PMC article.
-
Optimal co-segmentation of tumor in PET-CT images with context information.IEEE Trans Med Imaging. 2013 Sep;32(9):1685-97. doi: 10.1109/TMI.2013.2263388. Epub 2013 May 16. IEEE Trans Med Imaging. 2013. PMID: 23693127 Free PMC article.
-
Region detection by minimizing intraclass variance with geometric constraints, global optimality, and efficient approximation.IEEE Trans Med Imaging. 2011 Mar;30(3):814-27. doi: 10.1109/TMI.2010.2095870. Epub 2010 Nov 29. IEEE Trans Med Imaging. 2011. PMID: 21118766 Free PMC article.
References
-
- Amir A, Kashi R, Netanyalm NS. Analyzing quantitative databases: Image is everything. Proc. 27th Int. Conf. Very Large Data Bases (VLDB),; Rome, Italy. 2001. pp. 89–98.
-
- Asano T, Chen DZ, Katoh N, Tokuyama T. Efficient algorithms for optimization-based image segmentation. Int J Comput Geom Appl. 2001;11(2):145–166.
-
- Barbu A, Zhu S. Graph partition by Swendsen–Wang cuts. Proc. Int. Conf. Computer Vision; Nice, France. 2003. pp. 320–327.
-
- Benezit F, Cour T, Shi J. Spectral segmentation with multi-scale graph decomposition. Proc. IEEE Computer Society Conf. Computer Vision and Pattern Recognition (CVPR); Jun, 2005. pp. 1124–1131.
-
- Boykov Y, Kolmogorov V. Computing geodesics and minimal surfaces via graph cuts. Proc. Int. Conf. Computer Vision (ICCV); Nice, France. Oct, 2003. pp. 26–33.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous
