Antibiotic dose impact on resistance selection in the community: a mathematical model of beta-lactams and Streptococcus pneumoniae dynamics

Abstract

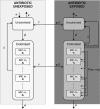
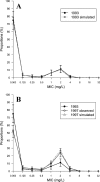
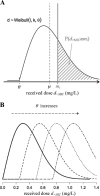
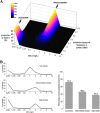
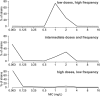
Streptococcus pneumoniae is a major pathogen in the community and presents high rates of resistance to the available antibiotics. To prevent antibiotic treatment failure caused by highly resistant bacteria, increasing the prescribed antibiotic dose has recently been suggested. The aim of the present study was to assess the influence of beta-lactam prescribed doses on the emergence of resistance and selection in the community. A mathematical model was constructed by combining S. pneumoniae pharmacodynamic and population-dynamic approaches. The received-dose heterogeneity in the population was specifically modeled. Simulations over a 50-year period were run to test the effects of dose distribution and antibiotic exposure frequency changes on community resistance patterns, as well as the accuracy of the defined daily dose as a predictor of resistance. When the frequency of antibiotic exposure per year was kept constant, dose levels had a strong impact on the levels of resistance after a 50-year simulation. The lowest doses resulted in a high prevalence of nonsusceptible strains (> or =70%) with MICs that were still low (1 mg/liter), whereas high doses resulted in a lower prevalence of nonsusceptible strains (<40%) and higher MICs (2 mg/liter). Furthermore, by keeping the volume of antibiotics constant in the population, different patterns of use (low antibiotic dose and high antibiotic exposure frequency versus high dose and low frequency) could lead to markedly different rates of resistance distribution and prevalence (from 10 to 100%). Our results suggest that pneumococcal resistance patterns in the community are strongly related to the individual beta-lactam doses received: limiting beta-lactam use while increasing the doses could help reduce the prevalence of resistance, although it should select for higher levels of resistance. Surveillance networks are therefore encouraged to collect both daily antibiotic exposure frequencies and individual prescribed doses.

FIG. 1.

Model structure outline. The population was divided into several groups or compartments, according to S. pneumoniae colonization (rows) and antibiotic exposure (columns). Uncolonized individuals could become colonized at rate β per contact with colonized individuals (X_i and Y_i) independently of antibiotic exposure or the antibiotic resistance of the colonizing strains. Independently of their carriage status, individuals could be exposed during average time 1/γ to a distribution of β-lactam doses at frequency ϕ. Decolonization could result from either natural immunity (after average time 1/λ) or antibiotic exposure, provided that the prescribed dose exceeded the MIC for the pneumococcal strains carried. For each group Y_i of carriers of strains with MIC m_i, the probability that β-lactam exposure would clear the carriage was P(d_>MIC ≥ m_i). Finally, resistance emerged or the MIC increased from m_i to m_j only in antibiotic-exposed individuals with an increasing MIC rate P(i → j).

FIG. 2.

Dose distribution calibration and validation. (A) The parameters and the distribution were calibrated to fit the observed resistance patterns in 1993 (17), the model was initialized with all strains being susceptible, and the simulation was run for a 50-year period. (B) Comparison of the simulated and the observed MIC distributions from 1993 to 1997 with the estimated dose distribution and parameters (17).

FIG. 3.

Simulated dose distributions. (A) In the model, antibiotic dose (d_>MIC) followed a W(l, k, θ) distribution, with l being the scale, k the shape, and θ the location of the d_>MIC distribution. At the population level, for each group Y_i of individuals carrying pneumococcal strains with MIC m_i, the probability that the β-lactam would clear carriage was P[d_>MIC ≥ m_i | d_>MIC ∼ W(l, k, θ)]. (B) In the simulations, the dose exposure distribution changed by shifting the W(0.43, 2, θ) distribution to the right, with the value of θ ranging from 0 to 1. Therefore, the mean dose varied with θ, i.e., d_mean = E[d_>MIC] = θ + l × Γ[1 + (1/k)], while variance and shape were not affected: SD = σ[d_>MIC] = l² × Γ[1 + (2/k)] − (E[d_>MIC] − θ)². In the model, the doses received were defined as the maximum value that the serum concentrations were exceeded for more than 50% of the time, meaning that they could be equivalent to the maximum MIC for which treatment was efficient.

FIG. 4.

Impact over 50 years of changes in antibiotic exposure frequency and dose distribution on the susceptibility patterns of pneumococci. Starting with only susceptible strains, simulations were performed and the prevalence rates of all nonsusceptibility levels among carriers after 50 years were drawn as a function of specific parameters. (A) Impact of antibiotic exposure frequency. The prevalence of nonsusceptible strains among carriers is depicted as a function of the resistance level (MIC) and antibiotic exposure frequency, ϕ. The dose distribution was fixed [W(l = 0.43, k = 2, θ = 0.4)], and the antibiotic exposure frequency in the community varied from 0 to 0.8 prescription per year. When ϕ increased, more nonsusceptible strains were selected and a second MIC distribution peak appeared. The MICs for nonsusceptible strains, represented by the peak, increased with ϕ: for an average frequency of 1 prescription every 3 years, the nonsusceptible strain prevalence after 50 years was 35%, whereas for an average 1 prescription every 2 years, it was >90%. (B) Dose impact. For a fixed ϕ of 0.33 prescription per year, dose distribution changes were characterized by θ, the location of the Weibull distribution, corresponding to the lowest dose received in the population. The prevalence of nonsusceptible strains among carriers is depicted as a function of the resistance level (MIC) (left) and overall (right) for three dose distributions θ of 0, 0.4, and 0.8 mg/liter, corresponding to low, medium, and high doses, respectively (d_mean = 0.38, 0.78, and 1.18 mg/liter, respectively). For the lowest, intermediate, and high doses, the prevalence of nonsusceptible strains could exceed 70%, with the MIC distribution peaking at about 1 mg/liter; could exceed 45%, with the MIC peak spanning 1 to 2 mg/liter; and could exceed 37%, with the MIC being about 2 mg/liter, respectively.

FIG. 5.

Simulation for a fixed DDD. The DDD indicator (i_DDD) was set at i_DDD = ϕ⁰ × d_mean⁰ = 0.33 × 0.78 = 0.26. Starting with all strains being susceptible, 50-year simulations were computed for three different antibiotic exposure frequencies (ϕ) and d_mean combinations for which ϕ × d_mean = i_DDD = constant. The prevalence of nonsusceptible strains among carriers is depicted as a function of the resistance level (MIC) for each simulation combination. For these graphs, the parameter sets {ϕ (number of prescriptions per year), θ (mg/liter)} were, from top to bottom, {0.53, 0.1}, {0.33, 0.4}, and {0.25, 0.65}, respectively.