Exploring the Sensitivity of Horn's Parallel Analysis to the Distributional Form of Random Data
- PMID: 20234802
- PMCID: PMC2838619
- DOI: 10.1080/00273170902938969
Exploring the Sensitivity of Horn's Parallel Analysis to the Distributional Form of Random Data
Abstract
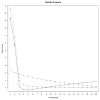
Horn's parallel analysis (PA) is the method of consensus in the literature on empirical methods for deciding how many components/factors to retain. Different authors have proposed various implementations of PA. Horn's seminal 1965 article, a 1996 article by Thompson and Daniel, and a 2004 article by Hayton, Allen, and Scarpello all make assertions about the requisite distributional forms of the random data generated for use in PA. Readily available software is used to test whether the results of PA are sensitive to several distributional prescriptions in the literature regarding the rank, normality, mean, variance, and range of simulated data on a portion of the National Comorbidity Survey Replication (Pennell et al., 2004) by varying the distributions in each PA. The results of PA were found not to vary by distributional assumption. The conclusion is that PA may be reliably performed with the computationally simplest distributional assumptions about the simulated data.
Figures
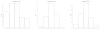
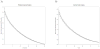
Similar articles
-
Commentary on "Exploring the Sensitivity of Horn's Parallel Analysis to the Distributional Form of Random Data".Multivariate Behav Res. 2009 May-Jun;44(3):389-95. doi: 10.1080/00273170902939033. Multivariate Behav Res. 2009. PMID: 26754401 No abstract available.
-
High Horn's index score predicts poor outcomes in patients with Clostridium difficile infection.J Hosp Infect. 2011 Sep;79(1):23-6. doi: 10.1016/j.jhin.2011.04.027. Epub 2011 Jun 22. J Hosp Infect. 2011. PMID: 21700363
-
Detection of outliers in reference distributions: performance of Horn's algorithm.Clin Chem. 2005 Dec;51(12):2326-32. doi: 10.1373/clinchem.2005.058339. Epub 2005 Oct 13. Clin Chem. 2005. PMID: 16223885
-
Improving Methods for Discrete Choice Experiments to Measure Patient Preferences [Internet].Washington (DC): Patient-Centered Outcomes Research Institute (PCORI); 2021 Mar. Washington (DC): Patient-Centered Outcomes Research Institute (PCORI); 2021 Mar. PMID: 38386769 Free Books & Documents. Review.
-
Examining distributional characteristics of clusters.Bull Soc Sci Med Grand Duche Luxemb. 2010;Spec No 1(1):14-39. Bull Soc Sci Med Grand Duche Luxemb. 2010. PMID: 20653176 Review.
Cited by
-
Loneliness in Intimate Relationships Scale (LIRS): Development and Validation.Int J Environ Res Public Health. 2022 Oct 10;19(19):12970. doi: 10.3390/ijerph191912970. Int J Environ Res Public Health. 2022. PMID: 36232275 Free PMC article.
-
Data-driven human transcriptomic modules determined by independent component analysis.BMC Bioinformatics. 2018 Sep 17;19(1):327. doi: 10.1186/s12859-018-2338-4. BMC Bioinformatics. 2018. PMID: 30223787 Free PMC article.
-
Factor Retention in Exploratory Factor Analysis With Missing Data.Educ Psychol Meas. 2022 Jun;82(3):444-464. doi: 10.1177/00131644211022031. Epub 2021 Jun 11. Educ Psychol Meas. 2022. PMID: 35444335 Free PMC article.
-
Characterizing intergenic transcription at RNA polymerase II binding sites in normal and cancer tissues.Cell Genom. 2023 Sep 29;3(10):100411. doi: 10.1016/j.xgen.2023.100411. eCollection 2023 Oct 11. Cell Genom. 2023. PMID: 37868033 Free PMC article.
-
Loaded: Gun involvement among opioid users.Drug Alcohol Depend. 2018 Jun 1;187:205-211. doi: 10.1016/j.drugalcdep.2018.03.015. Epub 2018 Apr 16. Drug Alcohol Depend. 2018. PMID: 29680676 Free PMC article.
References
-
- Allen SJ, Hubbard R. Regression equations for the latent roots of random data correlation matrices with unities on the diagonal. Multivariate Behavioral Research. 1986;21:393–96. - PubMed
-
- Benjamini Y, Hochberg Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society Series B (Methodological) 1995;57:289–300.
-
- Benjamini Y, Yekutieli D. The Control of the False Discovery Rate in Multiple Testing under Dependency. The Annals of Statistics. 2001;29:1165–1188.
-
- Browne MW, Cudeck R. Alternative Ways of Assessing Model Fit. Sociological Methods & Research. 1992;21:230.
-
- Cattell RB. The scree test for the number of factors. Multivariate Behavioral Research. 1966;1:245–276. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases
