Searching for autocoherence in the cortical network with a time-frequency analysis of the local field potential

Abstract

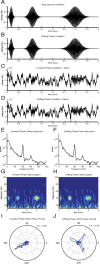
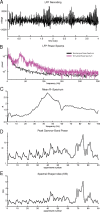
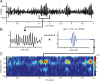
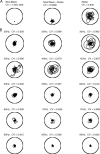
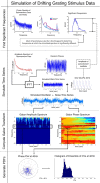
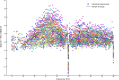
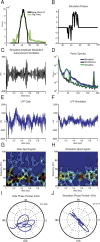
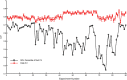
Gamma-band peaks in the power spectrum of local field potentials (LFP) are found in multiple brain regions. It has been theorized that gamma oscillations may serve as a 'clock' signal for the purposes of precise temporal encoding of information and 'binding' of stimulus features across regions of the brain. Neurons in model networks may exhibit periodic spike firing or synchronized membrane potentials that give rise to a gamma-band oscillation that could operate as a 'clock'. The phase of the oscillation in such models is conserved over the length of the stimulus. We define these types of oscillations to be 'autocoherent'. We investigated the hypothesis that autocoherent oscillations are the basis of the experimentally observed gamma-band peaks: the autocoherent oscillator (ACO) hypothesis. To test the ACO hypothesis, we developed a new technique to analyze the autocoherence of a time-varying signal. This analysis used the continuous Gabor transform to examine the time evolution of the phase of each frequency component in the power spectrum. Using this analysis method, we formulated a statistical test to compare the ACO hypothesis with measurements of the LFP in macaque primary visual cortex, V1. The experimental data were not consistent with the ACO hypothesis. Gamma-band activity recorded in V1 did not have the properties of a 'clock' signal during visual stimulation. We propose instead that the source of the gamma-band spectral peak is the resonant V1 network driven by random inputs.

Figure 1.

A, Amplitude-modulated autocoherent sine wave at 40 Hz. B, Amplitude-modulated drifting phase sine wave at 40 Hz. C, Amplitude-modulated autocoherent sine wave at 40 Hz added to simulated spontaneous V1 LFP activity. D, Amplitude-modulated drifting phase sine wave at 40 Hz added to simulated spontaneous V1 LFP activity. E, Power spectrum of signal C. F, Power spectrum of signal D. G, Spectrogram of signal C. H, Spectrogram of signal D. I, Phase portrait at 40 Hz of signal C. J, Phase portrait at 40 Hz of signal D.

Figure 2.

Gamma-Band power spectrum from 90 experiments A, The time course of a 4 s LFP during visual stimulation by a drifting grating. B, Power spectra of the LFP: spontaneous LFP spectrum (black); LFP spectrum of the response to a drifting grating stimulus (magenta) from A. C, R-spectrum of the data from 10 to 100 Hz averaged over all 90 experiments. D, Peak value of the R-spectrum in the gamma-band for each experiment. E, Spectral shape index (SSI) for each experiment. The slow trend upwards in D and E are not meaningful and probably reflect increasing skill of the experimenters.

Figure 3.

Continuous Gabor transform (CGT) analysis of LFP data. A, The time course of a 4 s LFP recording (same example data as in Fig. 2A). B, Schematic diagram of continuous Gabor transform. C, The amplitude spectrum from the continuous Gabor transform of the time course in A.

Figure 4.

A, Phase portraits for a constant amplitude sine wave, a constant amplitude sine wave in noise, and noise only. B, Phase portraits of the data shown in Figure 3 for frequencies in the gamma band. Each portrait is for a 4 s period.

Figure 5.

Flow chart for the generation of the simulated CV PDF for the constant amplitude ACO null hypothesis.

Figure 6.

Statistical test of null hypothesis I: constant amplitude autocoherent oscillator (ACO). The differences between the CVs of the data at each frequency with significantly elevated power under visual stimulation for all 90 experiments and the simulated 99th percentiles of CV with respect to the constant amplitude ACO null model are shown. Differences greater than zero correspond to the rejection of the constant amplitude ACO hypothesis.

Figure 7.

Simulation of null model: amplitude-modulated autocoherent oscillator from LFP data. A, Power of stimulated LFP data at frequencies significantly elevated from the spontaneous activity (green); power spectrum of the simulated amplitude-modulated ACO is a symmetric power spectrum fitted to the LFP data (black). B, Phase spectrum of simulated amplitude-modulated ACO. C, Simulated amplitude-modulated ACO signal, A(t), generated by the inverse Fourier transform of the spectra in A (black) and B. D, Power spectra of spontaneous activity of LFP data (black), stimulated LFP data (blue), and simulated null model: simulated amplitude-modulated ACO added to simulated spontaneous activity (green). E, Voltage time series of LFP data. F, Voltage time series of simulated null model: simulated amplitude-modulated ACO added to simulated spontaneous activity. G, Spectrogram of E. H, Spectrogram of F. I, Phase portrait of LFP data (subplot E) at the estimated carrier frequency. J, Phase portrait of simulated null model (subplot F) at the estimated carrier frequency.

Figure 8.

Statistical test of null hypothesis II: amplitude-modulated autocoherent oscillator (ACO). Circular variances of the data with standard errors at the estimated carrier frequencies (red), and 99th percentile of the CV PDF of the simulated amplitude-modulated ACO null model (black).

Figure 9.

A, Time course of a 3 s EEG recording exhibiting an autocoherent oscillation at 11 Hz (black), and fitted autocoherent alpha oscillation (green). B, Phase portrait at 11 Hz of the EEG recording plotted in A (blue), and mean phase of the 11 Hz trajectory (black arrow). C, Power spectrum of EEG recording plotted in A.

Figure 10.

Output of the numerical simulation of a model network of 10 inhibitory neurons connected all-to-all. A, Population average voltage time course convolved with an inhibitory synaptic conductance kernel. B, Phase portrait and circular variance at 42 Hz of the time course plotted in A.