Multigenerational interstitial growth of biological tissues

Abstract

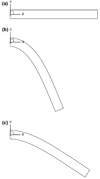
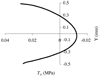
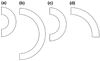
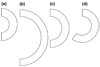
This study formulates a theory for multigenerational interstitial growth of biological tissues whereby each generation has a distinct reference configuration determined at the time of its deposition. In this model, the solid matrix of a growing tissue consists of a multiplicity of intermingled porous permeable bodies, each of which represents a generation, all of which are constrained to move together in the current configuration. Each generation's reference configuration has a one-to-one mapping with the master reference configuration, which is typically that of the first generation. This mapping is postulated based on a constitutive assumption with regard to that generations' state of stress at the time of its deposition. For example, the newly deposited generation may be assumed to be in a stress-free state, even though the underlying tissue is in a loaded configuration. The mass content of each generation may vary over time as a result of growth or degradation, thereby altering the material properties of the tissue. A finite element implementation of this framework is used to provide several illustrative examples, including interstitial growth by cell division followed by matrix turnover.

Fig. 1

Growth of a cantilever beam. a Stress-free reference configuration of T₁ (first generation). b Loaded configuration of T₁, also loaded configuration of T₂, following growth of second generation. c Unloaded (residually stressed) configuration of T₂

Fig. 2

Effective normal stress distribution T_xx at fixed end of cantilever beam

Fig. 3

Thick-walled tube, growth in inner rim only; due to symmetry, only the right side of the tube is modeled. a T₁ in stress-free configuration. b T₁ (and T₂) with internal pressurization. c T₂ in unloaded configuration. d T₂ in unloaded configuration, after radial cut; the opening angle is positive

Fig. 4

Thick-walled tube, growth in outer rim only. a T₁ in stress-free configuration. b T₁ (and T₂) with internal pressurization. c T₂ in unloaded configuration. d T₂ in unloaded configuration, after radial cut; the opening angle is negative

Fig. 5

Thick-walled tube, homogeneous growth. a T₁ in stress-free configuration. b T₁ (and T₂) with internal pressurization. c T₂ in unloaded configuration. d T₂ in unloaded configuration, after radial cut; the opening angle is negative

Fig. 6

Radial distribution of residual circumferential normal effective stress at apex (Θ = π/2), for thick-walled tube in its second generation (T₂) unloaded configuration, before and after radial cut. a Inner rim growth; b outer rim growth; c homogeneous growth

Fig. 7

Growth by cell division, followed by matrix turnover. J^s indicates the relative change in volume of T over time; p is the interstitial fluid pressure