Bipedal locomotion in crawling cells

Abstract

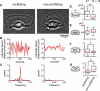
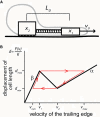
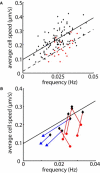
Many complex cellular processes from mitosis to cell motility depend on the ability of the cytoskeleton to generate force. Force-generating systems that act on elastic cytoskeletal elements are prone to oscillating instabilities. In this work, we have measured spontaneous shape and movement oscillations in motile fish epithelial keratocytes. In persistently polarized, fan-shaped cells, retraction of the trailing edge on one side of the cell body is out of phase with retraction on the other side, resulting in periodic lateral oscillation of the cell body. We present a physical description of keratocyte oscillation in which periodic retraction of the trailing edge is the result of elastic coupling with the leading edge. Consistent with the predictions of this model, the observed frequency of oscillation correlates with cell speed. In addition, decreasing the strength of adhesion to the substrate reduces the elastic force required for retraction, causing cells to oscillate with higher frequency at relatively lower speeds. These results demonstrate that simple elastic coupling between movement at the front of the cell and movement at the rear can generate large-scale mechanical integration of cell behavior.

Figure 1

Periodic shape and movement oscillations. A locomoting keratocyte was imaged at 5-s intervals for 6 min, and the frequency of oscillation of cell body, cell length, and edge velocity were measured by fast Fourier transform. (A) Individual frames from the movie are shown at 25-s intervals; the outline of the cell from the preceding image is superimposed on each frame. Scale bar, 10 μm. (B) The position of the cell body centroid plotted in two dimensions (red line), fit to a smooth curve (black line). (C) Lateral displacement of the cell body. The distance between the cell body centroid and the fit line shown in B is plotted over time. (D) Cell length on the left (blue line) and right (green line) sides of the cell body over time. (E) Power spectra for cell body (red line) and cell length (blue and green lines) oscillations. The power of each transform is plotted versus frequency. (F) Edge velocity map. Cell outlines were extracted from each image and resampled such that point 0 is the cell rear and point 100 is the cell front. The velocity at each point on the cell perimeter is plotted over time. Negative velocities (blue) are retractions and positive values (red) are protrusions. (G) Velocities of the trailing edge to the left of the cell body (point 175; upper graph), the center of the leading edge (point 100; middle graph), and the trailing edge to the right of the cell body (point 25; lower graph) are plotted over time. (H) Power spectra for the velocities of the leading edge and trailing edge on either side of the cell body. The frequency of oscillation of the cell body, cell length, and trailing edge velocity for this cell is ∼42 s.

Figure 2

Oscillating cells are faster and more coherent than nonoscillating cells. A population of 50 randomly selected cells were imaged at 5-s intervals for 10 min, and the frequency of lateral cell body oscillation was measured by fast Fourier transform. Of the 50 cells, 37 oscillated with significant power (see Methods). (A–C) Representative examples of an oscillating cell (right) and a nonoscillating cell (left) are shown. (A) Phase images. (B) Lateral displacement of the cell body. The cell body position for each cell was fit to a smooth curve, and the distance between the fit line and the cell body position is plotted over time. (C) Power spectra for the cell body oscillations. (D–G) Box and whisker plots for cell speed (D), area (E), aspect ratio (F), and front roughness (G) for populations of oscillating and nonoscillating cells. The plots indicate the 25th percentile (lower bound), median (red line), 75th percentile (upper bound), and observations within 1.5 times the interquartile range (whiskers). Asterisks indicate significant differences between the oscillating and nonoscillating populations (^∗p < 0.05; ^∗∗p < 0.005).

Figure 3

One-dimensional model for keratocyte oscillation. (A) The leading edge (position x₁) moves forward with constant velocity v₀. The trailing edge (position x₂) adheres to the substrate. The leading and trailing edges are connected by an elastic element with stiffness K and rest length L₀. (B) Schematic plot of d, the displacement of the cell length from rest, as a function of v, the velocity of the trailing edge. At small velocity, ν < ν₁, the rear of the cell forms adhesions to the substrate and moves more slowly than the front, and the cell stretches, with displacement d = F(ν)/K ≈ βν. When the speed of the trailing edge reaches ν₁, the adhesions between the rear of the cell and substrate rupture, and v quickly increases to ν_max. As the rear of the cell then begins to slow down, at large ν > ν₂ the length of the cell decreases with d ≈ αν. When ν < ν₂, adhesions reform between the cell and the substrate, the velocity of the rear slows to ν_min, and the length of the cell again increases with d ≈ βν.

Figure 4

Cell body oscillation correlates with cell speed. (A) The frequency of oscillation for a population of control cells (black diamonds, n = 98) and cells treated with 100 μg/ml RGD (red circles, n = 23) was measured by fast Fourier transform and is plotted versus cell speed. Cell speed significantly correlates with frequency of oscillation for both control (solid line, R² = 0.44, p < 0.01) and RGD-treated cells (dashed line, R² = 0.3, p = 0.01), with the RGD-treated cells oscillating at higher frequencies at relatively lower speeds. To determine whether the two populations were significantly different, we compared the residuals from the control fit line for both the control and RGD-treated populations; the mean residual value for the RGD population (−0.08 ± 0.01) was significantly different from the mean residual for the control population (0 ± 0.006, p < 10⁻⁹, Student's t-test). (B) Oscillation frequency for individual cells is plotted versus cell speed before (black diamonds) and after treatment with either 10 nM latrunculin A (blue triangles) or 100 μg/ml RGD peptides (red circles). The solid black line is the fit line from the control population in A.

Figure 5

Two-dimensional model. (A) The leading edge is connected to the trailing edge (positions x_2l and x_2r) by springs $\overline{K}$ and K, which have rest lengths ${\overline{L}}_0$ and L₀, respectively. x_2l and x_2r are connected to each other by spring K_w, with rest length W. (B) Simulated cell length (distance between x_l and x_2l or x_2r) oscillations for ν₀= 0.2 μm/s, shown for both left (blue) and right (green) sides. (C) The frequency of oscillation correlates with ν₀ for a wide range of values for g. (D) State diagram of cell length oscillations. Equations 4–7 were evaluated numerically at the indicated values for g and K_w (circles). To determine whether the oscillations were stable or irregular, the time correlation coefficient, C, was calculated between the left, L(t), and right, R(t + P) sides, where P is the time lag between the two sides (see Methods). Oscillations were defined as stable antiphase (pink shading), with relative phase lag between 0.4 and 0.5, and C > 0.8; stable in-phase (gray shading), with relative phase lag between 0 and 0.1, and C > 0.8; and having irregular motion (no shading), defined as C < 0.8. g₀ = 1 s² nN/μm; K_w0 = 1 nN/μm. Parameter values used in B–D are W = 20 μm, L₀ = 10 μm, ${\overline{L}}_0$ = 5 μm, v₁ = 0.08 μm/s, ν₂ =1 μm/s, α = 0.5 s, β = 25 s, γ = 4 s, K = 1 nN/μm, $\overline{K}$ = 10 nN/μm, K_w = 10 nN/μm, and g = 0.1 s² nN/μm.rrruu.