Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2010 Jun 1;50(11):1041-7.
doi: 10.1016/j.visres.2010.03.012. Epub 2010 Mar 23.

Age-dependent Fourier model of the shape of the isolated ex vivo human crystalline lens

Raksha Urs  1 , Arthur Ho, Fabrice Manns, Jean-Marie Parel
Affiliations

Age-dependent Fourier model of the shape of the isolated ex vivo human crystalline lens

Raksha Urs et al. Vision Res. .

Abstract

Purpose: To develop an age-dependent mathematical model of the zero-order shape of the isolated ex vivo human crystalline lens, using one mathematical function, that can be subsequently used to facilitate the development of other models for specific purposes such as optical modeling and analytical and numerical modeling of the lens.

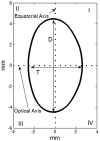
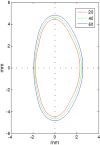
Methods: Profiles of whole isolated human lenses (n=30) aged 20-69, were measured from shadow-photogrammetric images. The profiles were fit to a 10th-order Fourier series consisting of cosine functions in polar-co-ordinate system that included terms for tilt and decentration. The profiles were corrected using these terms and processed in two ways. In the first, each lens was fit to a 10th-order Fourier series to obtain thickness and diameter, while in the second, all lenses were simultaneously fit to a Fourier series equation that explicitly include linear terms for age to develop an age-dependent mathematical model for the whole lens shape.

Results: Thickness and diameter obtained from Fourier series fits exhibited high correlation with manual measurements made from shadow-photogrammetric images. The root-mean-squared-error of the age-dependent fit was 205 microm. The age-dependent equations provide a reliable lens model for ages 20-60 years.

Conclusion: The contour of the whole human crystalline lens can be modeled with a Fourier series. Shape obtained from the age-dependent model described in this paper can be used to facilitate the development of other models for specific purposes such as optical modeling and analytical and numerical modeling of the lens.

PubMed Disclaimer

Figures

Figure 1
Figure 1
The co-ordinate system for the Fourier model. The lens anterior surface was placed in quadrants II and III and the posterior surface was placed in the quadrants I and IV. T and D represent the thickness and diameter of the lens.
Figure 2
Figure 2
The original lens contour (black), lens contour fit to Equation 1 (green) and the adjusted lens contour (red). (2a) Shows lens contour in Cartesian coordinates and (2b) in polar coordinates for contour extracted from shadow-photogrammetric images of a 28 year-old human crystalline lens that was 3 days post mortem.
Figure 2
Figure 2
The original lens contour (black), lens contour fit to Equation 1 (green) and the adjusted lens contour (red). (2a) Shows lens contour in Cartesian coordinates and (2b) in polar coordinates for contour extracted from shadow-photogrammetric images of a 28 year-old human crystalline lens that was 3 days post mortem.
Figure 3
Figure 3
Linear regression of thickness (T) and diameter (D) of the human crystalline lens with age yielded T = 3.8 (±0.9) + 0.01(±0.004) × Age (R=0.45, p=0.01) and D = 8.6 (±0.3) + 0.02(±0.01) × Age (R=0.53, p=0.002).
Figure 4
Figure 4
Bland-Altman plots for thickness (4a) and diameter (4b) of the lens measured from shadow-photogrammetric images and from Fourier function fits. Most measurements were within 2 standard deviations of the mean measurement error. The mean measurement error was 0.02±0.04 mm for the thickness and 0.01±0.1 mm for the diameter. These results indicate that measurements from both methods are the same.
Figure 4
Figure 4
Bland-Altman plots for thickness (4a) and diameter (4b) of the lens measured from shadow-photogrammetric images and from Fourier function fits. Most measurements were within 2 standard deviations of the mean measurement error. The mean measurement error was 0.02±0.04 mm for the thickness and 0.01±0.1 mm for the diameter. These results indicate that measurements from both methods are the same.
Figure 5
Figure 5
Age-dependent Fourier model of 20 (red), 40 (green) and 60 (blue) year-old lenses
Figure 6
Figure 6
Figure shows raw lens contours (blue) of ages 20 (a), 32 (b), 42 (c), 48 (d), 53 (e) and 63 (f) years on which the corresponding shape obtained from the age-dependent Fourier lens model is superimposed (red).
Figure 6
Figure 6
Figure shows raw lens contours (blue) of ages 20 (a), 32 (b), 42 (c), 48 (d), 53 (e) and 63 (f) years on which the corresponding shape obtained from the age-dependent Fourier lens model is superimposed (red).
Figure 6
Figure 6
Figure shows raw lens contours (blue) of ages 20 (a), 32 (b), 42 (c), 48 (d), 53 (e) and 63 (f) years on which the corresponding shape obtained from the age-dependent Fourier lens model is superimposed (red).
Figure 6
Figure 6
Figure shows raw lens contours (blue) of ages 20 (a), 32 (b), 42 (c), 48 (d), 53 (e) and 63 (f) years on which the corresponding shape obtained from the age-dependent Fourier lens model is superimposed (red).
Figure 6
Figure 6
Figure shows raw lens contours (blue) of ages 20 (a), 32 (b), 42 (c), 48 (d), 53 (e) and 63 (f) years on which the corresponding shape obtained from the age-dependent Fourier lens model is superimposed (red).
Figure 6
Figure 6
Figure shows raw lens contours (blue) of ages 20 (a), 32 (b), 42 (c), 48 (d), 53 (e) and 63 (f) years on which the corresponding shape obtained from the age-dependent Fourier lens model is superimposed (red).
Figure 7
Figure 7
Graph shows effect of the number of coefficients included in the Fourier series on the RMSE fit of a lens surface. Overall RMSE values converged at order 10 and did not decrease significantly for orders higher than 10.
Figure 8
Figure 8
(8a) Anterior (Ra) and Posterior (Rp) radii of curvature obtained from conic function fits of raw lens contours. Linear regression of curvatures as a function of age yielded Ra = 5.6 (±1.4) + 0.08 (±0.03) × Age (R = 0.47; p=0.009) and Rp = -3.81 (±0.51) - 0.05 (±0.01) × Age (R = -0.62; p=0.0002). (8b) Anterior (Ra) and Posterior (Rp) radii of curvature obtained from conic function fits of the age-dependent Fourier lens model. Linear regression of curvatures as a function of age yielded Ra = 3.9 (±0.1) + 0.11 (±0.002) × Age (R = 0.99; p<.0001) and Rp = -3.96 (±0.004) - 0.04 (±7E-5) × Age (R = -0.99; p<.0001).
Figure 8
Figure 8
(8a) Anterior (Ra) and Posterior (Rp) radii of curvature obtained from conic function fits of raw lens contours. Linear regression of curvatures as a function of age yielded Ra = 5.6 (±1.4) + 0.08 (±0.03) × Age (R = 0.47; p=0.009) and Rp = -3.81 (±0.51) - 0.05 (±0.01) × Age (R = -0.62; p=0.0002). (8b) Anterior (Ra) and Posterior (Rp) radii of curvature obtained from conic function fits of the age-dependent Fourier lens model. Linear regression of curvatures as a function of age yielded Ra = 3.9 (±0.1) + 0.11 (±0.002) × Age (R = 0.99; p<.0001) and Rp = -3.96 (±0.004) - 0.04 (±7E-5) × Age (R = -0.99; p<.0001).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Augusteyn RC, Rosen AM, Borja D, Ziebarth NM, Parel JM. Biometry of primate lenses during immersion in preservation media. Molecular Vision. 2006;12:740–747. - PubMed
    1. Augusteyn RC. Growth of the human eye lens. Molecular Vision. 2007;13:252–257. - PMC - PubMed
    1. Augusteyn RC. Growth of the lens: in vitro observations. Clinical and Experimental Optometry. 2008;91:226–239. - PubMed
    1. Borja D, Manns F, Ho A, Ziebarth NM, Rosen AM, Jain R, Amelinckx A, Arrieta E, Augusteyn RC, Parel JM. Optical power of the isolated human crystalline lens. Investigative Ophthalmology and Visual Science. 2008;49:2541–2548. - PMC - PubMed
    1. Chien CM, Huang T, Schachar RA. A mathematical expression for the human crystalline lens. Comprehensive Therapy. 2003;29:245–258. - PubMed

Publication types