Neural computation of visual imaging based on Kronecker product in the primary visual cortex

Abstract

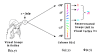
Background: What kind of neural computation is actually performed by the primary visual cortex and how is this represented mathematically at the system level? It is an important problem in the visual information processing, but has not been well answered. In this paper, according to our understanding of retinal organization and parallel multi-channel topographical mapping between retina and primary visual cortex V1, we divide an image into orthogonal and orderly array of image primitives (or patches), in which each patch will evoke activities of simple cells in V1. From viewpoint of information processing, this activated process, essentially, involves optimal detection and optimal matching of receptive fields of simple cells with features contained in image patches. For the reconstruction of the visual image in the visual cortex V1 based on the principle of minimum mean squares error, it is natural to use the inner product expression in neural computation, which then is transformed into matrix form.

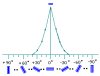
Results: The inner product is carried out by using Kronecker product between patches and function architecture (or functional column) in localized and oriented neural computing. Compared with Fourier Transform, the mathematical description of Kronecker product is simple and intuitive, so is the algorithm more suitable for neural computation of visual cortex V1. Results of computer simulation based on two-dimensional Gabor pyramid wavelets show that the theoretical analysis and the proposed model are reasonable.

Conclusions: Our results are: 1. The neural computation of the retinal image in cortex V1 can be expressed to Kronecker product operation and its matrix form, this algorithm is implemented by the inner operation between retinal image primitives and primary visual cortex's column. It has simple, efficient and robust features, which is, therefore, such a neural algorithm, which can be completed by biological vision. 2. It is more suitable that the function of cortical column in cortex V1 is considered as the basic unit of visual image processing (such unit can implement basic multiplication of visual primitives, such as contour, line, and edge), rather than a set of tiled array filter. Fourier Transformation is replaced with Kronecker product, which greatly reduces the computational complexity. The neurobiological basis of this idea is that a visual image can be represented as a linear combination of orderly orthogonal primitive image containing some local feature. In the visual pathway, the image patches are topographically mapped onto cortex V1 through parallel multi-channels and then are processed independently by functional columns. Clearly, the above new perspective has some reference significance to exploring the neural mechanisms on the human visual information processing.

Figure 1

Visual image R (x, y) is divided into M × N local patches according to a ganglion cell's receptive field.

Figure 2

Selective matching between r_i,j (a) (a horizontal edge) and different receptive fields in functional columns. The receptive field g_i,j (b) with horizontal orientation response strongly.

Figure 3

Convolution operation for horizontal lines (A) and vertical lines (B) in image patches in R(x, y).

Figure 4

Functional columns as basic information processing units. (A) Eight representative types of receptive fields in function columns in V1; (B) Orientations range from 0° to 180° with a same interval of 10°; (C) An example of receptive field calculated by formula (9).

Figure 5

Optimal matching between a patch (upper right corner of the hat) and receptive fields of specific orientations in cortical modules [B_k,l (s)]_{K × L}.

Figure 6

Orthogonal division of a visual image.

Figure 7

Three representations of eight types of receptive fields in function columns in V1 calculated by Gabor function, in which orientations 0°, 10°, 20°, ⋯, 180° in turn.

Figure 8

Image reconstruction by topological mapping and Kronecker product. (A) Source image Lenna; (B) Retinal image [R_i,j(2^h a)]_{M × N}; (C) Receptive fields array B_k,l(s) of functional columns in V1; (D) The whole activated pattern of receptive field image [Φ_i,j(b)]_{M × N} ; (E),(F) and (G) A part of activated pattern [Φ_i,j (b)]_{M × N} in V1 calculated by formulas 14-16 (upper right corner of the hat).

Figure 9

Result (only of the upper right part of the hat shown) corresponding to the damaged function columns at i = 5, j = 9; i = 7, j = 2; i = 11, j = 15.