Quantifying aggregated uncertainty in Plasmodium falciparum malaria prevalence and populations at risk via efficient space-time geostatistical joint simulation
- PMID: 20369009
- PMCID: PMC2848537
- DOI: 10.1371/journal.pcbi.1000724
Quantifying aggregated uncertainty in Plasmodium falciparum malaria prevalence and populations at risk via efficient space-time geostatistical joint simulation
Abstract
Risk maps estimating the spatial distribution of infectious diseases are required to guide public health policy from local to global scales. The advent of model-based geostatistics (MBG) has allowed these maps to be generated in a formal statistical framework, providing robust metrics of map uncertainty that enhances their utility for decision-makers. In many settings, decision-makers require spatially aggregated measures over large regions such as the mean prevalence within a country or administrative region, or national populations living under different levels of risk. Existing MBG mapping approaches provide suitable metrics of local uncertainty--the fidelity of predictions at each mapped pixel--but have not been adapted for measuring uncertainty over large areas, due largely to a series of fundamental computational constraints. Here the authors present a new efficient approximating algorithm that can generate for the first time the necessary joint simulation of prevalence values across the very large prediction spaces needed for global scale mapping. This new approach is implemented in conjunction with an established model for P. falciparum allowing robust estimates of mean prevalence at any specified level of spatial aggregation. The model is used to provide estimates of national populations at risk under three policy-relevant prevalence thresholds, along with accompanying model-based measures of uncertainty. By overcoming previously unchallenged computational barriers, this study illustrates how MBG approaches, already at the forefront of infectious disease mapping, can be extended to provide large-scale aggregate measures appropriate for decision-makers.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
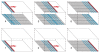
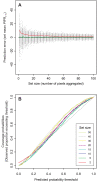
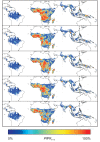
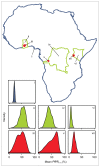
References
-
- Hay SI, Graham AJ, Rogers DJ. Global mapping of infectious diseases: methods, examples and emerging applications. London: Academic Press; 2006. 446 - PubMed
-
- Snow RW, Marsh K, LeSueur D. The need for maps of transmission intensity to guide malaria control in Africa. Parasitol Today. 1996;12:455–457.
-
- Diggle PJ, Tawn JA, Moyeed RA. Model-based geostatistics. J Roy Stat Soc C-App. 1998;47:299–326.
-
- Diggle P, Ribeiro PJ. Model-based Geostatistics. New York: Springer; 2007. 228
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

