Detecting dynamical boundaries from kinematic data in biomechanics

Abstract

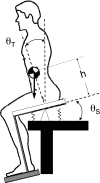
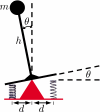
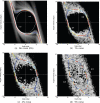
Ridges in the state space distribution of finite-time Lyapunov exponents can be used to locate dynamical boundaries. We describe a method for obtaining dynamical boundaries using only trajectories reconstructed from time series, expanding on the current approach which requires a vector field in the phase space. We analyze problems in musculoskeletal biomechanics, considered as exemplars of a class of experimental systems that contain separatrix features. Particular focus is given to postural control and balance, considering both models and experimental data. Our success in determining the boundary between recovery and failure in human balance activities suggests this approach will provide new robust stability measures, as well as measures of fall risk, that currently are not available and may have benefits for the analysis and prevention of low back pain and falls leading to injury, both of which affect a significant portion of the population.

Figure 1

Detecting dynamical boundaries from measured data. (a) Schematic showing two example trajectories, both of which start in the stable region and end in the unstable region. By analyzing the motion of points along the trajectory appropriately, we can find the boundary or recovery envelope between stable and unstable (i.e., failure) motions. The divergence between two points (b and c) on opposite sides of a recovery envelope separatrix is larger than the divergence of points on the same side [pairs (a, b) and (c, d)], which tend to move together over short times. (b) An observable separatrix forms from simulated experimental trials of the wobble chair. The separatrix is found as a LCS, i.e., a ridge in the FTLE field.

Figure 2

Flowchart depicting how separatrices (as LCSs) are traditionally determined. The underlying vector fields are unavailable in musculoskeletal experiments; only the resulting time series (i.e., trajectories) are available. Therefore we must consider an algorithm that starts with trajectories (the boxed steps) while assuming that trajectories were generated by a, perhaps unknown, vector field.

Figure 3

The wobble chair is an unstable sitting apparatus designed to isolate the movement of the low back to determine torso stability. (Figure is adapted from Fig. 1 in Ref. and Fig. 1a in Ref. .) The angle θ_S is the angle the seat makes with the horizontal and θ_T is the angle the torso makes with the vertical.

Figure 4

Recovery envelopes: a new tool in the evaluation of fall risk. Shown schematically, the boundary between the states corresponding to stable walking (recovery) and falling (failure) is given by a recovery envelope (thick line). We assume the state space is equipped with a metric and suggest that the minimum state space distance between a subject’s kinematic variability and their recovery envelope (d_min) can be used as a measure of their falling risk.

Figure 5

(a) A trajectory ϕ(t;x₀) and a neighboring trajectory ϕ(t;x₀+δx₀). (b) The state transition matrix is a deformation gradient about the reference trajectory describing how an initially spherical blob of surrounding states deforms into an ellipsoid.

Figure 6

Estimating the maximum FTLE at a location in phase space by evaluating the growth of perturbation vectors in multiple state space directions. We make the assumption that the maximum FTLE dominates the evolution of the perturbation vectors.

Figure 7

Main steps of the algorithm. From the FTLE field (left panel) the ridge points are calculated and aggregated toward the ridge axis (central panel). Thereafter, the points are appropriately connected (right panel) in order to create continuous curves.

Figure 8

Subject balances on the wobble chair moving the lumbar region of her torso to maintain stability.

Figure 9

One DOF model for the wobble chair. In the simplified model the angle between the seat and the torso is fixed and control is applied at the base. This is an approximation to more complex system where torso flexion causes rear spring compression and extension causes front spring compression for effective base applied control.

Figure 10

The FTLE field and detected boundaries (ridges) are shown for a full sampling of phase space for the reduced order wobble chair model at four values of the noise. The boundary separating the stable and unstable regions of phase space is shown. The boundary has two parts (roughly an upper and a lower part), and we give the average flux across each. Each boundary is made up of elements color coded according to the amount of flux across the element: low flux (higher strength) is lighter, high flux (lower strength) is darker. The solid closed curve in (a) is the theoretical boundary for zero noise.

Figure 11

A time-series data set generated from 20 simulated experimental trials. (a) Time plot shows each trial beginning from the state space origin. (b) The trials shown as trajectories in phase space.

Figure 12

(a) A portion of a dynamical boundary found by analyzing the FTLE field resulting from the trajectories of Fig. 11. Only portions of the complete boundary are accessible by this method. The flux for the upper-right and lower-left portions is also shown. (b) A comparison of the dynamical boundaries from the partial sample (solid) and full-grid data (dotted).

Figure 13

(a) Model of a person sitting on the wobble chair. Components of the lower body contribute to segment one, while components of the upper body make up segment two. (b) Simplified model of a person sitting on the wobble chair. Vectors c_i are from joint i to the COM of segment i, while L₁ is the vector from joint 1 to joint 2. The deflection of the lower body and seat from the balanced configuration is θ₁ and the deflection of the upper body from the vertical position is θ₂. Forces are applied to the stabilizing springs providing effective base control of the combined COM as the body pivots at the lumbar spine (L4-L5) during flexion and extension of the torso.

Figure 14

Recovery envelopes and basin of stability from 4D simulated data. FTLE field for simulated wobble chair data seen in two different two-dimensional slices of the full 4D state space (the slice is at the origin in the two other dimensions): (a) $\left({\theta }_1,{\dot{\theta }}_1\right)$ and (b) $\left({\theta }_2,{\dot{\theta }}_2\right)$. Notice the ridge of high FTLE surrounding a region of low FTLE. This ridge is a slice of a LCS, a recovery envelope which bounds—and from which we can measure the size of—the basin of stability. Although only two dimensions are shown for visualization purposes, the basin volume can be computed in the full 4D state space.