Quantitative analysis of single particle trajectories: mean maximal excursion method

Abstract

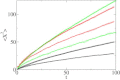
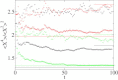
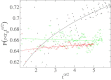
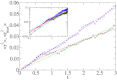
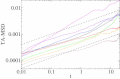
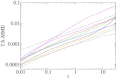
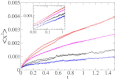
An increasing number of experimental studies employ single particle tracking to probe the physical environment in complex systems. We here propose and discuss what we believe are new methods to analyze the time series of the particle traces, in particular, for subdiffusion phenomena. We discuss the statistical properties of mean maximal excursions (MMEs), i.e., the maximal distance covered by a test particle up to time t. Compared to traditional methods focusing on the mean-squared displacement we show that the MME analysis performs better in the determination of the anomalous diffusion exponent. We also demonstrate that combination of regular moments with moments of the MME method provides additional criteria to determine the exact physical nature of the underlying stochastic subdiffusion processes. We put the methods to test using experimental data as well as simulated time series from different models for normal and anomalous dynamics such as diffusion on fractals, continuous time random walks, and fractional Brownian motion.

Figure 1

MSD 〈r²(t)〉 and second MME moment $\langle r_{\max }^2\rangle$ as function of time t (arbitrary units) for the three simulated time series (1000 trajectories of 100 steps each), each with anomalous diffusion exponent α = 0.7. The power-law fits produce, for two-dimensional percolation data, α = 0.64 (MSD, depicted by black ×) and α = 0.73 (MME, black Δ); for CTRW data, α = 0.67 (MSD, red ×) and α = 0.71 (MME, red Δ); and for FBM data, α = 0.72 (MSD, green ×) and α′ = 0.79 (MME, green Δ, expected value α′ ≈ 0.74).

Figure 2

Regular and MME moment ratios 〈r⁴〉/〈r²〉² and $\langle r_{\max }^4\rangle /{\langle r_{\max }^2\rangle }^2$ as function of time (a.u.) for the three simulated sets (diffusion on a fractal, FBM, and CTRW). Each set consists of 1000 trajectories with 100 steps each. (Black Δ) MME ratio for the diffusion on a two-dimensional percolation cluster; the data do not converge to the expected value 1.29 (black horizontal line). The same behavior is observed for the regular moment ratio (black +), for which the expected value is 1.77 (short black line). This discrepancy is likely due to the confinement of the percolation cluster on a 250 × 250 network: the random walker quickly reaches the boundaries, and the convergence occurs toward the equilibrium distribution, not toward the free space propagator. (Red Δ) MME ratio for the CTRW process, converging to 1.97 (red horizontal line). We also plot the regular moment ratio (red +); these are more irregular and converge to 2.66 (short red line). For FBM, the MME ratio (green Δ) converges to the estimated value of Eq. 11, 1.33 (green horizontal line), and the regular ratio (green +) oscillates around the Brownian value 2 (short green line).

Figure 3

Probability to be in a growing sphere of radius r₀t^α/2 as function of t^α/2 for the three simulated sets (a.u.). This analysis is based on the previously fitted values of α. Results: Two-dimensional critical percolation (black ×) produces d – d_f ≈ 0.11, i.e., d_f ≈ 1.89 (exact value 91:48 ≈ 1.896). The CTRW set (red ×) gives d – d_f ≈ 0.01 instead of 0, and the FBM set (green ×) leads to d – d_f ≈ – 0.004 instead of 0.

Figure 4

Analysis of an experimental set of 67 trajectories, the longest consisting of 210 points, for quantum dots freely diffusing in a solvent. MSD (black ×), fitted by a power law with exponents α = 0.81 (red line). We also show a fit with fixed exponent α = 1 (green line, expected behavior for BM). MME (blue ×), fitted by a power law (red line, α = 1.02). Time is in s; distances are in μm². (Inset) Double-logarithmic plot of the same data.

Figure 5

Lipid granules diffusing in a yeast cell. Eight trajectories, between 5515 and 19,393 frames' long. Log-log plot of the time-averaged MSD as a function of lag time (continuous lines), and A₀t^0.4 (dotted lines). Time is scaled in s, and time-averaged MSD is in μm².

Figure 6

Lipid granules diffusing in a yeast cell. Log-log plot of the time-averaged second MME moment of the data from Fig. 5 as function of lag time (continuous lines), and A₀t^0.5 (dotted lines). Time is scaled in s; the ordinate is in μm².

Figure 7

Lipid granules diffusing in a yeast cell. Five-hundred-and-twenty-six subtrajectories of 100 steps extracted from the experimental set of five trajectories, which are between 5515 and 19,393 frames' long. Ensemble-averaged MSD (black •) fitted by a power law (α = 0.41, black line), and ensemble-averaged MME (red •), fitted with a power law (α = 0.55, red line). We verified that creating 350 trajectories of 150 steps instead of 100 does not change the exponents obtained from the MSD or the second MME moment (× instead of • symbols). Because one of the trajectories had a steeper slope than the others, we repeated the same analysis without this trajectory. The new subset contained 445 trajectories of 100 steps, or 296 of 150 steps (MSD in blue leading to α = 0.42, second MME moment in magenta producing α = 0.51). Time is in s; the ordinate is measured in μm². (Inset) Double-logarithmic plot of the same data.