Reducing number entry errors: solving a widespread, serious problem
- PMID: 20375037
- PMCID: PMC2935596
- DOI: 10.1098/rsif.2010.0112
Reducing number entry errors: solving a widespread, serious problem
Abstract
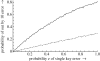
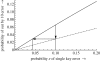
Number entry is ubiquitous: it is required in many fields including science, healthcare, education, government, mathematics and finance. People entering numbers are to be expected to make errors, but shockingly few systems make any effort to detect, block or otherwise manage errors. Worse, errors may be ignored but processed in arbitrary ways, with unintended results. A standard class of error (defined in the paper) is an 'out by 10 error', which is easily made by miskeying a decimal point or a zero. In safety-critical domains, such as drug delivery, out by 10 errors generally have adverse consequences. Here, we expose the extent of the problem of numeric errors in a very wide range of systems. An analysis of better error management is presented: under reasonable assumptions, we show that the probability of out by 10 errors can be halved by better user interface design. We provide a demonstration user interface to show that the approach is practical.To kill an error is as good a service as, and sometimes even better than, the establishing of a new truth or fact. (Charles Darwin 1879 [2008], p. 229).
Figures

Similar articles
-
Unreliable numbers: error and harm induced by bad design can be reduced by better design.J R Soc Interface. 2015 Sep 6;12(110):0685. doi: 10.1098/rsif.2015.0685. J R Soc Interface. 2015. PMID: 26354830 Free PMC article.
-
Reducing wrong patient selection errors: exploring the design space of user interface techniques.AMIA Annu Symp Proc. 2014 Nov 14;2014:1056-65. eCollection 2014. AMIA Annu Symp Proc. 2014. PMID: 25954415 Free PMC article.
-
Technology-induced errors: where do they come from and what can we do about them?Stud Health Technol Inform. 2013;194:20-6. Stud Health Technol Inform. 2013. PMID: 23941924
-
Reducing medication errors and increasing patient safety: case studies in clinical pharmacology.J Clin Pharmacol. 2003 Jul;43(7):768-83. J Clin Pharmacol. 2003. PMID: 12856392 Review.
-
Importance of practical simulation training for troubleshooting the heart-lung machine.J Artif Organs. 2009;12(2):67-72. doi: 10.1007/s10047-008-0454-z. Epub 2009 Jun 18. J Artif Organs. 2009. PMID: 19536622 Review.
Cited by
-
Assessing the Usability of Six Data Entry Mobile Interfaces for Caregivers: A Randomized Trial.JMIR Hum Factors. 2015 Dec 15;2(2):e15. doi: 10.2196/humanfactors.4093. JMIR Hum Factors. 2015. PMID: 27025648 Free PMC article.
-
Unreliable numbers: error and harm induced by bad design can be reduced by better design.J R Soc Interface. 2015 Sep 6;12(110):0685. doi: 10.1098/rsif.2015.0685. J R Soc Interface. 2015. PMID: 26354830 Free PMC article.
-
Reducing wrong patient selection errors: exploring the design space of user interface techniques.AMIA Annu Symp Proc. 2014 Nov 14;2014:1056-65. eCollection 2014. AMIA Annu Symp Proc. 2014. PMID: 25954415 Free PMC article.
-
Development and Validation of Automated Visual Field Report Extraction Platform Using Computer Vision Tools.Front Med (Lausanne). 2021 Apr 29;8:625487. doi: 10.3389/fmed.2021.625487. eCollection 2021. Front Med (Lausanne). 2021. PMID: 33996848 Free PMC article.
-
Interactive numerals.R Soc Open Sci. 2017 Apr 26;4(4):160903. doi: 10.1098/rsos.160903. eCollection 2017 Apr. R Soc Open Sci. 2017. PMID: 28484609 Free PMC article.
References
-
- Arnold K., Gosling J. 1996. The Java programming language. Reading, MA: Addison-Wesley.
-
- Darwin C. 1879. [2008] Letter to A. S. Wilson, March 5, 1879. In More letters of Charles Darwin, vol. 2 (eds. Darwin F., Seward A. C.). Charleston, SC: BiblioBazaar.
-
- Degani A. 2001. Taming HAL: designing interfaces beyond 2001. New York, NY: Palgrave.
-
- Food and Drug Administration (FDA). 2009 MedSun: medical product safety network. MedSun Newsletter no. 33. Cardinal Health Alaris 8100, 18 November 2008. See www.accessdata.fda.gov/scripts/cdrh/cfdocs/medsun/news/newsletter.cfm?ne.... (Accessed March 2010).
-
- Fox A., Cliff D., Hoare T., Fordham M., Masterson-Jones N., McDermid J., Rodd M., Thomas M. 2009. Engineering values in IT. London, UK: The Royal Academy of Engineering.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

