Economically optimal timing for crop disease control under uncertainty: an options approach
- PMID: 20375038
- PMCID: PMC2935598
- DOI: 10.1098/rsif.2010.0056
Economically optimal timing for crop disease control under uncertainty: an options approach
Abstract
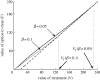
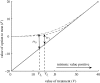
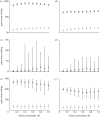
Severe large-scale disease and pest infestations in agricultural regions can cause significant economic damage. Understanding if and when disease control measures should be taken in the presence of risk and uncertainty is a key issue. We develop a framework to examine the economically optimal timing of treatment. The decision to treat should only be undertaken when the benefits exceed the costs by a certain amount and not if they are merely equal to or greater than the costs as standard net-present-value (NPV) analysis suggests. This criterion leads to a reduction in fungicide use. We investigate the effect of the model for disease progress on the value required for immediate treatment by comparing two standard models for disease increase (exponential and logistic growth). Analyses show that the threshold value of benefits required for immediate release of treatment varies significantly with the relative duration of the agricultural season, the intrinsic rate of increase of the disease and the level of uncertainty in disease progression. In comparing the performance of the delay strategy introduced here with the conventional NPV approach, we show how the degree of uncertainty affects the benefits of delaying control.
Figures
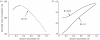
References
-
- Burdon J. J., Chilvers G. A. 1982. Host density as a factor in plant disease ecology. Annu. Rev. Phytopathol. 20, 143–166. (10.1146/annurev.py.20.090182.001043) - DOI
-
- Cook R. J., Hims M. J., Vaughan T. B. 1999. Effects of fundicide spray timing on winter wheat disease control. Plant Pathol. 48, 33–50. (10.1046/j.1365-3059.1999.00319.x) - DOI
-
- Dixit A. K., Pindyck R. S. 1994. Investment under uncertainty. Princeton, NJ: Princeton University Press.
-
- Forsyth M. 2000. On estimating the option value of preserving a wilderness area. Can. J. Econ. 33, 413–434. (10.1111/0008-4085.00022) - DOI
-
- Gilligan C. A. 2002. An epidemiological framework for disease management. Adv. Bot. Res. 38, 1–64.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

