Mechanical Stability Determines Stress Fiber and Focal Adhesion Orientation
- PMID: 20376295
- PMCID: PMC2849636
- DOI: 10.1007/s12195-009-0093-3
Mechanical Stability Determines Stress Fiber and Focal Adhesion Orientation
Abstract
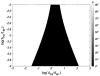
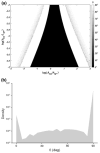
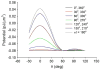
It is well documented in a variety of adherent cell types that in response to anisotropic signals from the microenvironment cells alter their cytoskeletal organization. Previous theoretical studies of these phenomena were focused primarily on the elasticity of cytoskeletal actin stress fibers (SFs) and of the substrate while the contribution of focal adhesions (FAs) through which the cytoskeleton is linked to the external environment has not been considered. Here we propose a mathematical model comprised of a single linearly elastic SF and two identical linearly elastic FAs of a finite size at the endpoints of the SF to investigate cytoskeletal realignment in response to uniaxial stretching of the substrate. The model also includes the contribution of the chemical potential energies of the SF and the FAs to the total potential energy of the SF-FA assembly. Using the global (Maxwell's) stability criterion, we predict stable configurations of the SF-FA assembly in response to substrate stretching. Model predictions obtained for physiologically feasible values of model parameters are consistent with experimental data from the literature. The model shows that elasticity of SFs alone can not predict their realignment during substrate stretching and that geometrical and elastic properties of SFs and FAs need to be included.
Figures




Similar articles
-
A Model for Stress Fiber Realignment Caused by Cytoskeletal Fluidization During Cyclic Stretching.Cell Mol Bioeng. 2011 Mar 1;4(1):67-80. doi: 10.1007/s12195-010-0152-9. Cell Mol Bioeng. 2011. PMID: 21666861 Free PMC article.
-
Durotaxis as an elastic stability phenomenon.J Biomech. 2008;41(6):1289-94. doi: 10.1016/j.jbiomech.2008.01.008. Epub 2008 Mar 4. J Biomech. 2008. PMID: 18308324
-
Movement of stress fibers away from focal adhesions identifies focal adhesions as sites of stress fiber assembly in stationary cells.Cell Motil Cytoskeleton. 2007 Dec;64(12):966-76. doi: 10.1002/cm.20237. Cell Motil Cytoskeleton. 2007. PMID: 17868136
-
From stress fiber to focal adhesion: a role of actin crosslinkers in force transmission.Front Cell Dev Biol. 2024 Aug 13;12:1444827. doi: 10.3389/fcell.2024.1444827. eCollection 2024. Front Cell Dev Biol. 2024. PMID: 39193363 Free PMC article. Review.
-
Probing mechanical principles of focal contacts in cell-matrix adhesion with a coupled stochastic-elastic modelling framework.J R Soc Interface. 2011 Sep 7;8(62):1217-32. doi: 10.1098/rsif.2011.0157. Epub 2011 Jun 1. J R Soc Interface. 2011. PMID: 21632610 Free PMC article. Review.
Cited by
-
Biomechanics of cell reorientation in a three-dimensional matrix under compression.Exp Cell Res. 2017 Jan 1;350(1):253-266. doi: 10.1016/j.yexcr.2016.12.002. Epub 2016 Dec 2. Exp Cell Res. 2017. PMID: 27919745 Free PMC article.
-
Formation of contractile networks and fibers in the medial cell cortex through myosin-II turnover, contraction, and stress-stabilization.Cytoskeleton (Hoboken). 2015 Jan;72(1):29-46. doi: 10.1002/cm.21207. Epub 2015 Feb 7. Cytoskeleton (Hoboken). 2015. PMID: 25641802 Free PMC article.
-
A Statistical Mechanics Approach to Describe Cell Reorientation Under Stretch.Bull Math Biol. 2023 May 30;85(7):60. doi: 10.1007/s11538-023-01161-4. Bull Math Biol. 2023. PMID: 37249663 Free PMC article.
-
Cell reorientation under cyclic stretching.Nat Commun. 2014 May 30;5:3938. doi: 10.1038/ncomms4938. Nat Commun. 2014. PMID: 24875391 Free PMC article.
-
A Model for Stress Fiber Realignment Caused by Cytoskeletal Fluidization During Cyclic Stretching.Cell Mol Bioeng. 2011 Mar 1;4(1):67-80. doi: 10.1007/s12195-010-0152-9. Cell Mol Bioeng. 2011. PMID: 21666861 Free PMC article.
References
-
- Balaban NQ, Schwarz US, Riveline D, Goichberg P, Tzur G, Sabanay I, Mahalu D, Safran S, Bershadsky A, Addadi L, Geiger B. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat Cell Biol. 2001;3:466–472. - PubMed
-
- Costa KD, Hucker WJ, Yin FCP. Buckling of actin stress fibers: a new wrinkle in the cytoskeletal tapestry. Cell Motil Cytoskeleton. 2002;52:266–274. - PubMed
-
- Dartsch PC, Hämmerle H. Orientation response of arterial smooth muscle cells to mechanical stimulation. Eur J Cell Biol. 1986;41:339–346. - PubMed
-
- De R, Zemel A, Safran SA. Dynamics of cell orientation. Nat Phys. 2007;3:655–659.
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

