Introduction to phasing
- PMID: 20382985
- PMCID: PMC2852296
- DOI: 10.1107/S0907444910006694
Introduction to phasing
Abstract
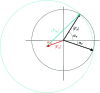
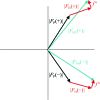
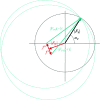
When collecting X-ray diffraction data from a crystal, we measure the intensities of the diffracted waves scattered from a series of planes that we can imagine slicing through the crystal in all directions. From these intensities we derive the amplitudes of the scattered waves, but in the experiment we lose the phase information; that is, how we offset these waves when we add them together to reconstruct an image of our molecule. This is generally known as the 'phase problem'. We can only derive the phases from some knowledge of the molecular structure. In small-molecule crystallography, some basic assumptions about atomicity give rise to relationships between the amplitudes from which phase information can be extracted. In protein crystallography, these ab initio methods can only be used in the rare cases in which there are data to at least 1.2 A resolution. For the majority of cases in protein crystallography phases are derived either by using the atomic coordinates of a structurally similar protein (molecular replacement) or by finding the positions of heavy atoms that are intrinsic to the protein or that have been added (methods such as MIR, MIRAS, SIR, SIRAS, MAD, SAD or combinations of these). The pioneering work of Perutz, Kendrew, Blow, Crick and others developed the methods of isomorphous replacement: adding electron-dense atoms to the protein without disturbing the protein structure. Nowadays, methods from small-molecule crystallography can be used to find the heavy-atom substructure and the phases for the whole protein can be bootstrapped from this prior knowledge. More recently, improved X-ray sources, detectors and software have led to the routine use of anomalous scattering to obtain phase information from either incorporated selenium or intrinsic sulfurs. In the best cases, only a single set of X-ray data (SAD) is required to provide the positions of the anomalous scatters, which together with density-modification procedures can reveal the structure of the complete protein.
Figures
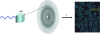

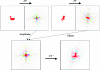

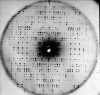

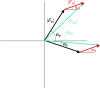
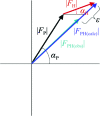
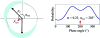

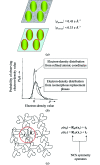
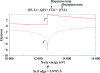
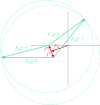
 m|F
P|exp(iαbest)× exp(−2πi
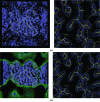
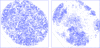
h·x). (b) A small section of the map with the final structure superimposed.
m|F
P|exp(iαbest)× exp(−2πi
h·x). (b) A small section of the map with the final structure superimposed.









References
-
- Abrahams, J. P. & Leslie, A. G. W. (1996). Acta Cryst. D52, 30–42. - PubMed
-
- Adams, P. D., Grosse-Kunstleve, R. W., Hung, L.-W., Ioerger, T. R., McCoy, A. J., Moriarty, N. W., Read, R. J., Sacchettini, J. C., Sauter, N. K. & Terwilliger, T. C. (2002). Acta Cryst. D58, 1948–1954. - PubMed
-
- Beevers, C. A. & Lipson, H. (1934). Proc. R. Soc. London A, 146, 570–582.
-
- Blow, D. M. (2002). Protein Crystallography for Biologists. Oxford University Press.
-
- Blow, D. M. & Crick, F. H. C. (1959). Acta Cryst.12, 794–802.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

