A mechanical model of actin stress fiber formation and substrate elasticity sensing in adherent cells
- PMID: 20385838
- PMCID: PMC2867880
- DOI: 10.1073/pnas.0912739107
A mechanical model of actin stress fiber formation and substrate elasticity sensing in adherent cells
Abstract
Tissue cells sense and respond to the stiffness of the surface on which they adhere. Precisely how cells sense surface stiffness remains an open question, though various biochemical pathways are critical for a proper stiffness response. Here, based on a simple mechanochemical model of biological friction, we propose a model for cell mechanosensation as opposed to previous more biochemically based models. Our model of adhesion complexes predicts that these cell-surface interactions provide a viscous drag that increases with the elastic modulus of the surface. The force-velocity relation of myosin II implies that myosin generates greater force when the adhesion complexes slide slowly. Then, using a simple cytoskeleton model, we show that an external force applied to the cytoskeleton causes actin filaments to aggregate and orient parallel to the direction of force application. The greater the external force, the faster this aggregation occurs. As the steady-state probability of forming these bundles reflects a balance between the time scale of bundle formation and destruction (because of actin turnover), more bundles are formed when the cytoskeleton time-scale is small (i.e., on stiff surfaces), in agreement with experiment. As these large bundles of actin, called stress fibers, appear preferentially on stiff surfaces, our mechanical model provides a mechanism for stress fiber formation and stiffness sensing in cells adhered to a compliant surface.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

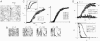
 ) decreases, indicating that there is a balance between stress fiber formation and breakdown. Bottom, steady-state stress fiber probability as a function of bundle size for four different values of actin turnover.
) decreases, indicating that there is a balance between stress fiber formation and breakdown. Bottom, steady-state stress fiber probability as a function of bundle size for four different values of actin turnover.
 ) of various sizes (N) as a function of the Young’s modulus of the surface. At low stiffness, no stress fibers form, while at high stiffnesses many, large stress fibers form. Inset, simulation results for stress fibers of 10 actin filaments (Gray, ± sd) and an interpolation between the results (Black). Details of the interpolation are in
) of various sizes (N) as a function of the Young’s modulus of the surface. At low stiffness, no stress fibers form, while at high stiffnesses many, large stress fibers form. Inset, simulation results for stress fibers of 10 actin filaments (Gray, ± sd) and an interpolation between the results (Black). Details of the interpolation are in References
-
- Engler AJ, Sen S, Sweeney HL, Discher DE. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. - PubMed
-
- Chan CE, Odde DJ. Traction dynamics of filipodia on compliant substrates. Science. 2008;322:1687–1691. - PubMed
-
- Discher DE, Janmey P, Wang Y. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–1143. - PubMed
-
- Geiger B, Spatz JP, Bershadsky AD. Environmental sensing through focal adhesions. Nat Rev Mol Cell Biol. 2009;10:21–23. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases
Research Materials

